练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若实数x、y、z满足x＋2y＋3z＝a(a为常数)，求x2＋y2＋z2的最小值．


    解：∵ (12＋22＋32)(x2＋y2＋z2)≥(x＋2y＋3z)2＝a2，即14(x2＋y2＋z2)≥a2，

    ∴ x2＋y2＋z2≥，即x2＋y2＋z2的最小值为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系，运用2×2列联表进行独立性检验，经计算K2＝7.069，则所得到的统计学结论是：有________的把握认为“学生性别与支持该活动有关系”(　　)

    附：

    P(K2≥k0)

    0.100

    0.050

    0.025

    0.010

    0.001

    k0

    2.706

    3.841

    5.024

    6.635

    10.828

    A.0.1%                            B．1%

    C．99%                            D．99.9%

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点M(a，b)在圆O：x2＋y2＝1外，则直线ax＋by＝1与圆O的位置关系是(　　)

    A．相切                           B．相交

    C．相离                           D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆E：＝1(a＞b＞0)，F1(－c,0)，F2(c,0)为椭圆的两个焦点，M为椭圆上任意一点，且|MF1|，|F1F2|，|MF2|构成等差数列，点F2(c,0)到直线l：x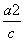＝的距离为3.

    (1)求椭圆E的方程；

    (2)若存在以原点为圆心的圆，使该圆的任意一条切线与椭圆E恒有两个交点A，B，且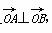，求出该圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求证：a2＋b2≥ab＋a＋b－1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x、y、z∈R，且满足x2＋y2＋z2＝1，x＋2y＋3z＝，求x＋y＋z的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “a<4”是“对任意的实数x，|2x－1|＋|2x＋3|≥a成立”的(　　)

    A．充分必要条件                    B．充分不必要条件

    C．必要不充分条件                  D．既非充分也非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求直线x＋y＝5在矩阵 对应的变换作用下得到的图形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将参数方程 化为普通方程，并说明它表示的图形．

    查看答案和解析>>

    同步练习册答案