练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （文）数列{an}满足an+1=
    n+2
    n
    an    （n∈N*），且a1=1．（1）求通项an；（2）记bn=
    1
    an
    ，数列{bn}的前n项和为Sn，求Sn．
    解（1）∵an+1=
    n+2
    n
    an    ，
    ∴
    an+1
    an
    =
    n+2
    n

    ∵a1=1
    ∴
    a2
    a1
    =
    3
    1
    ，
    a3
    a2
    =
    4
    2
    …
    an
    an-1
    =
    n+1
    n-1

    以上n-1个式子相乘可得，
    a2
    a1
    •
    a3
    a2
    …
    an
    an-1
    =
    3
    1
    ×
    4
    2
    ×
    5
    3
    …
    n-1
    n-3
    ×
    n
    n-2
    ×
    n+1
    n-1

    ∴
    an
    a1
    =
    n(n+1)
    1×2

    ∴an=
    n(n+1)
    2

    （2）∵bn=
    1
    an
    =
    2
    n(n+1)
    =2(
    1
    n
    -
    1
    n+1
    )
    Sn=2（1-
    1
    2
    +
    1
    2
    -
    1
    3
    +…+
    1
    n
    -
    1
    n+1
    ）=2（1-
    1
    n+1
    ）=
    2n
    n+1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （文）已知以a为首项的数列{an}满足：an+1=
    an-3，an＞3
    2an，an≤3.

    （1）若0＜an≤6，求证：0＜an+1≤6；
    （2）若a，k∈N﹡，求使an+k=an对任意正整数n都成立的k与a；
    （3）若a=
    3
    2m-1
    （m∈N﹡），试求数列{an}的前m项的和sm．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)设数列{an}满足条件：a1=a(a＞2)，且an+1=(n∈N*)．

    (1)证明：an＞2；

    (2)证明：a1+a2+…+an＜2(n+a-2)；

    (3)若xn=，求数列{xn}的通项公式

    (文)已知数列{an}和{bn}满足：a1=，且an+bn=1，bn+1=(n∈N*)．

    (1)求数列{an}与{bn}的通项公式；

    (2)设Sn=a1+a2+a2a3+…+anan+1．若对任意的n∈N*，不等式kSn＞bn恒成立，求正整数k的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)已知函数f(x)=(0＜x＜1)的反函数为f-1(x)，设它在点(n,f-1(n))(n∈N*)处

    的切线在Y轴上的截距为bn，数列{an}满足：a1=2，an+1=f-1(an)(n∈N*)．

    (1)求数列{an}的通项公式；

    (2)在数列{}中，仅当n=5时，取最小值，求A的取值范围；

    (3)令函数g(x)=f-1(x)(1+x)2，数列{cn}满足：c1=，cn+1=g(cn)(n∈N*)，求证：对于一切

    n≥2的正整数，都满足：1＜＜2．

    (文)已知函数f(x)：(0＜x＜1)的反函数为f-1(x)，数列{an}满足：a1=2，an+1=f-1(an) (n∈N*)．

    (1)求数列{an}的通项公式；

    (2)设函数g(x)=f-1(x)(1+x)2在点(n，g(n))(n∈N*)处的切线在Y轴上的截距为bn，求数列{bn}的通项公式；

    (3)在数列{bn+}中，仅当n=5时，bn+取最大值，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)已知函数f(x)=x,g(x)=ln(1+x),h(x)=.

    (1)证明当x＞0时,恒有f(x)＞g(x);

    (2)当x＞0时,不等式g(x)＞(k≥0)恒成立,求实数k的取值范围;

    (3)在x轴正半轴上有一动点D(x,0),过D作x轴的垂线依次交函数f(x)、g(x)、h(x)的图象于点A、B、C,O为坐标原点.试将△AOB与△BOC的面积比表示为x的函数m(x),并判断m(x)是否存在极值,若存在,求出极值;若不存在,请说明理由.

    (文)已知函数f(x)=,x∈(0,+∞),数列{an}满足a1=1,an+1=f(an);数列{bn}满足b1=1,bn+1=,其中Sn为数列{bn}的前n项和,n=1,2,3,….

    (1)求数列{an}和数列{bn}的通项公式;

    (2)设Tn=,证明Tn＜3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

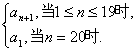    (理)设a1,a2,…,a20是首项为1,公比为2的等比数列.对于满足0≤k≤19的整数k,数列b1,b2,…,b20由bn=确定.记M=.

    (1)当k=1时,求M的值;

    (2)求M的最小值及相应的k的值.

    (文)设数列{an}的首项a1=a(a∈R),且an+1=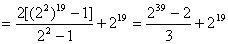n=1,2,3,….

    (1)若0＜a＜1,求a2、a3、a4、a5;

    (2)若0＜an＜4,证明0＜an+1＜4;

    (3)若0＜a≤2,求所有的正整数k,使得对于任意n∈N*,均有an+k=an成立.

    查看答案和解析>>

    同步练习册答案