练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．在R上定义运算⊕：x⊕y=（1-x）y，若不等式（x+a）⊕（x-a）＜4对任意实数x都成立，则a的取值范围是（-$\frac{3}{2}$，$\frac{5}{2}$）．

    分析 由运算⊕可得：不等式（x+a）⊕（x-a）＜4对任意实数x都成立?[1-（x+a）]（x-a）＜4对任意实数x成立，进行转化求解即可．

    解答 解：由运算⊕可得：不等式（x+a）⊕（x-a）＜4对任意实数x都成立?[1-（x+a）]（x-a）＜4对任意实数x成立，
    即x-a-x2+a2＜4，
    即x2-x-a2+a+4＞0恒成立，
    即判别式△=1-4（-a2+a+4）＜0恒成立，
    即4a2-4a-15＜0，
    则（2a+3）（2a-5）＜0，
    解得-$\frac{3}{2}$＜a＜$\frac{5}{2}$．
    ∴a的取值范围是（-$\frac{3}{2}$，$\frac{5}{2}$）．
    故答案为：$（-\frac{3}{2}，\frac{5}{2}）$

    点评 本题考查了新定义、恒成立问题的等价转化、一元二次不等式的解法等基础知识与基本技能方法，考查学生的运算和推理能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．在△ABC中，lga-1gb=1gsinB=-lg$\sqrt{2}$，B为锐角，则A的值是30°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成，如图1所示，AB⊥BC，且AB=2BC=2CD，将梯形ABCD沿着BC折起，形成如图2所示的几何体，且AB⊥平面BEC．
    （1）求证：平面ABE⊥平面ADE；
    （2）求二面角A-DE-B的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设直线y=kx与椭圆$\frac{x^2}{2}+{y^2}=1$相交于A，B两点，分别过A，B向x轴作垂线，若垂足恰为椭圆的两个焦点，则k=（　　）
    A．±1B．$±\frac{{\sqrt{2}}}{2}$C．$±\frac{1}{2}$D．$±\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图，在四棱柱ABCD-A1B1C1D1中，AC⊥B1D，BB1⊥底面ABCD，E、F、H分别为AD、CD、DD1的中点，EF与BD交于点G．
    （1）证明：平面ACD1⊥平面BB1D；
    （2）证明：GH∥平面ACD1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图所示，AE，DF是圆柱的两条母线，过AD作圆柱的截面交下底面于BC，且AD=BC，圆柱的高为2，底面半径为$\sqrt{3}$
    （Ⅰ）求证：平面AEB∥平面DFC
    （Ⅱ）求证：BC⊥AB
    （Ⅲ）求四棱锥E-ABCD体积最大时AD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

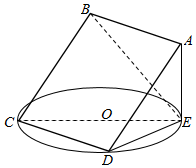    14．如图所示，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C，D的点，AE=3，圆O的直径为9．
    （Ⅰ）求证：平面ABCD⊥平面ADE； 
    （Ⅱ）求三棱锥D-ABE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若不等式x2+ax+1≥0对于一切x∈（0，$\frac{1}{2}$）恒成立，则a的取值范围是（　　）
    A．a≥0B．a≥-2C．a≥-$\frac{5}{2}$D．a≥-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知在△ABC中，点A（-1，0），B（0，$\sqrt{3}$），C（1，-2）．
    （Ⅰ）求边AB上高所在直线的方程；
    （Ⅱ）求△ABC的面积S△ABC．

    查看答案和解析>>

    同步练习册答案