
| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{4}$ |
分析 将直线方程与椭圆方程联立,得(1+2k2)x2=2.分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,说明A,B的横坐标是±1,即方程(1+2k2)x2=2的两个根为±1,代入求出k的值.
解答 解:将直线与椭圆方程联立,$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,
化简整理得(1+2k2)x2=2(*)
因为分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,
故方程的两个根为±1.代入方程(*),
得k=±$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了直线与椭圆的交点问题,方法是将直线与椭圆方程联立来求解,此方法是圆锥曲线中的重要思想方法.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,已知椭圆C的焦距为2,且|AB|=$\frac{\sqrt{6}}{2}$|BF|.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,已知椭圆C的焦距为2,且|AB|=$\frac{\sqrt{6}}{2}$|BF|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
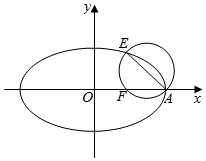 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 (B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )
(B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )| A. | PB⊥AD | B. | 平面PAB⊥平面PBC | ||
| C. | 直线BC∥平面PAE | D. | △PFB为等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com