
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.

(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
(1)见解析 (2)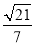 (3)
(3)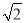
【解析】向量法
如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).

(1)证明:易得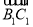 =(1,0,-1),
=(1,0,-1),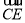 =(-1,1,-1),于是
=(-1,1,-1),于是 ·
·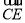 =0,所以B1C1⊥CE.
=0,所以B1C1⊥CE.
(2)  =(1,-2,-1).
=(1,-2,-1).
设平面B1CE的法向量m=(x,y,z),
则 即
即 消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1).
消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1).
由(1),B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,故 =(1,0,-1)为平面CEC1的一个法向量.
=(1,0,-1)为平面CEC1的一个法向量.
于是cos〈m, 〉=
〉= =
= =-
=-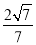 ,从而sin〈m,
,从而sin〈m, 〉=
〉=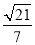 ,所以二面角B1CEC1的正弦值为
,所以二面角B1CEC1的正弦值为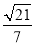 .
.
(3) 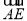 =(0,1,0),
=(0,1,0),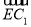 =(1,1,1),设
=(1,1,1),设 =λ
=λ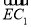 =(λ,λ,λ),0≤λ≤1,有
=(λ,λ,λ),0≤λ≤1,有 =
= +
+ =(λ,λ+1,λ).可取
=(λ,λ+1,λ).可取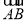 =(0,0,2)为平面ADD1A1的一个法向量.
=(0,0,2)为平面ADD1A1的一个法向量.
设θ为直线AM与平面ADD1A1所成的角,则
sin θ=|cos〈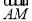 ,
, 〉|=
〉|= =
=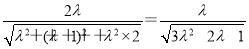 ,
,
于是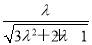 =
= ,解得λ=
,解得λ=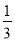 ,所以AM=
,所以AM=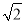 .
.
综合法

(1)证明 因为侧棱CC1⊥底面A1B1C1D1,B1C1?平面A1B1C1D1,所以CC1⊥B1C1.经计算可得B1E=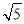 ,B1C1=
,B1C1= ,EC1=
,EC1=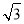 ,从而B1E2=B1
,从而B1E2=B1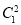 +E
+E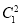 ,所以在△B1EC1中,B1C1⊥C1E,又CC1,C1E?平面CC1E,CC1∩C1E=C1,所以B1C1⊥平面CC1E,又CE?平面CC1E,故B1C1⊥CE.
,所以在△B1EC1中,B1C1⊥C1E,又CC1,C1E?平面CC1E,CC1∩C1E=C1,所以B1C1⊥平面CC1E,又CE?平面CC1E,故B1C1⊥CE.
(2)解 过B1作B1G⊥CE于点G,连接C1G.由(1),B1C1⊥CE,故CE⊥平面B1C1G,得CE⊥C1G,所以∠B1GC1为二面角B1-CE-C1的平面角.在△CC1E中,由CE=C1E= ,CC1=2,可得C1G=
,CC1=2,可得C1G= .
.
在Rt△B1C1G中,B1G=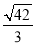 ,所以sin ∠B1GC1=
,所以sin ∠B1GC1=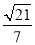 ,即二面角B1-CE-C1的正弦值为
,即二面角B1-CE-C1的正弦值为 .
.
(3)解 连接D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连接AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.设AM=x,从而在Rt△AHM中,有MH= x,AH=
x,AH= x.在Rt△C1D1E中,C1D1=1,ED1=
x.在Rt△C1D1E中,C1D1=1,ED1= ,得EH=
,得EH=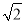 MH=
MH= x.
x.
在△AEH中,∠AEH=135°,AE=1,
由AH2=AE2+EH2-2AE·EHcos 135°,得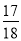 x2=1+
x2=1+ x2+
x2+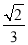 x,整理得5x2-2
x,整理得5x2-2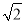 x-6=0,解得x=
x-6=0,解得x=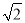 .
.
所以线段AM的长为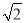 .
.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练8练习卷(解析版) 题型:选择题
已知非零向量a,b,c满足a+b+c=0,向量a与b的夹角为60°,且|a|=|b|=1,则向量a与c的夹角为( ).
A.30° B.60° C.120° D.150°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:填空题
已知点F是双曲线 =1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:选择题
已知椭圆E: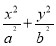 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
A. 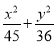 =1 B.
=1 B. 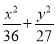 =1 C.
=1 C. 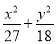 =1 D.
=1 D.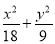 =1
=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
直线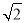 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0 B. C.
C. -1 D.
-1 D. +1
+1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知ABCD-A1B1C1D1为正方体,①( +
+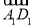 +
+ )2=3
)2=3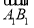 2;②
2;② ·(
·(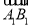 -
-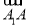 )=0;③向量
)=0;③向量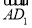 与向量
与向量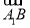 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|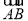 ·
·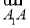 ·
·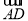 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.

(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
某四棱台的三视图如图所示,则该四棱台的体积是( ).
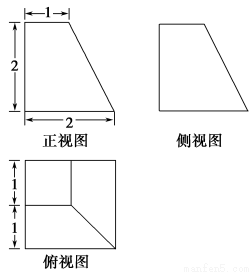
A.4 B. 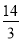 C.
C.  D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( ).
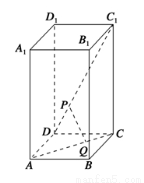
A. B.
B. 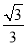 C.
C. 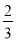 D.
D.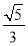
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com