
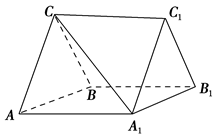
 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;

 ,
, ,
, ×22×
×22× =3.
=3. ,0),B(-1,0,0),C(0,0,
,0),B(-1,0,0),C(0,0, ),B1(-2,
),B1(-2, ,0),则
,0),则 =(1,0,
=(1,0, ),
), =(-1,
=(-1, ,0),
,0), =(0,-
=(0,- ,
, ),设n=(x,y,z)为平面BB1C1C的法向量,则
),设n=(x,y,z)为平面BB1C1C的法向量,则 即
即 所以n=(
所以n=( ,1,-1),
,1,-1), =
= =-
=- ,
, .
.

科目:高中数学 来源:不详 题型:解答题
 A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF= AB.
AB.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
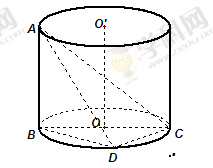
 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 上不与点
上不与点 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱 ,
, ,
, .
.
 ;
; 绕母线
绕母线 转动一周,求
转动一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围. 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com