Question

2．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积是（　　）

• A． 16π
• B． $\frac{81π}{4}$
• C． 9π
• D． $\frac{27π}{4}$

Answer 1

分析 正四棱锥P-ABCD的外接球的球心在它的高PE上，求出球的半径，求出球的表面积．

解答 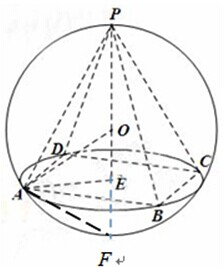解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，延长PE交球面于一点F，连接AE，AF，由球的性质可知△PAF为直角三角形且AE⊥PF，
根据平面几何中的射影定理可得PA²=PF•PE，
因为AE=$\frac{\sqrt{A{B}^{2}+B{C}^{2}}}{2}$=$\sqrt{2}$，
所以侧棱长PA=$\sqrt{P{E}^{2}+A{E}^{2}}$=3$\sqrt{2}$，PF=2R，
所以18=2R×4，所以R=$\frac{9}{4}$，
所以S=4πR²=$\frac{81π}{4}$
故选B．

点评 本题考查球的表面积，球的内接几何体问题，考查计算能力，是基础题．