
设f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
科目:高中数学 来源: 题型:
已知函数f(x)=cos x(sin x+cos x)-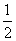 .
.
(1)若0<α<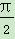 ,且sin α=
,且sin α=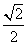 ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高度是46 m,则河流的宽度BC约等于________m.(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,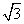 ≈1.73)
≈1.73)
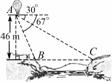 图13
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
若x>y,a>b,则在①a-x>b-y,②a+x>b+y,③ax>by,
④x-b>y-a,⑤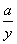 >
>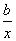 这五个式子中,恒成立的所有不等式的序号是________.
这五个式子中,恒成立的所有不等式的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com