练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1­3所示，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高度是46 m，则河流的宽度BC约等于________m．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80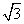，≈1.73)

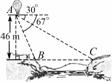    图1­3


    60　[解析] 过A点向地面作垂线，记垂足为D，则在Rt△ADB中，∠ABD＝67°，AD＝46 m，∴AB＝＝＝50(m)，

    在△ABC中，∠ACB＝30°，∠BAC＝67°－30°＝37°，AB＝50 m，

    由正弦定理得，BC＝＝60 (m)，

    故河流的宽度BC约为60 m.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x) = 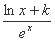（k为常数，e=2.71828……是自然对数的底数），曲线y= f(x)在点（1，f(1)）处的切线与x轴平行.

    （Ⅰ）求k的值；

    （Ⅱ）求f(x)的单调区间；

    （Ⅲ）设g(x)=(x2+x) 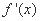,其中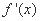为f(x)的导函数，证明：对任意x＞0，.

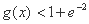    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝sin(ωx＋φ)的图像关于直线x＝对称，且图像上相邻两个最高点的距离为π.

    (1)求ω和φ的值；

    (2)若的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝sin(x＋θ)＋acos(x＋2θ)，其中a∈R，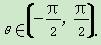

    (1)当a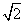＝，θ＝时，求f(x)在区间[0，π]上的最大值与最小值；

    (2)若，f(π)＝1，求a，θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，内角A，B，C所对的边分别是a，b，c.若c2＝(a－b)2＋6，C＝，则△ABC的面积是(　　)

    A．3  B.  C.  D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­5所示，在平面四边形ABCD中，AD＝1，CD＝2，AC＝.

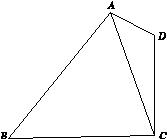
    图1­5

    (1)求cos∠CAD的值；

    (2)若cos∠BAD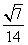＝－，sin∠CBA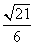＝，求BC的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，内角A，B，C所对的边分别为a，b，c，且满足a＝2sin A，＋＋＝0.

    (1)求c的值；

    (2)求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝ax2＋bx,1≤f(－1)≤2,2≤f(1)≤4，求f(－2)的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式的解集是（    ）

    A．        B．    C．   D．

    查看答案和解析>>

    同步练习册答案