
已知 函数f(x) =
函数f(x) = 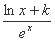 (k为常数,e=2.71828……是自然对数的底数),曲线y= f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e=2.71828……是自然对数的底数),曲线y= f(x)在点(1,f(1))处的切线与x轴平行.
(Ⅰ)求k的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=(x2+x) 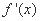 ,其中
,其中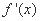 为f(x)的导函数,证明:对任意x>0,
为f(x)的导函数,证明:对任意x>0,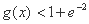 .
.
 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
方程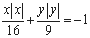 的曲线即为函数
的曲线即为函数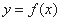 的图像,对于函数
的图像,对于函数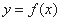 ,有如下结论:①
,有如下结论:①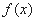 在R上单调递减;②函数
在R上单调递减;②函数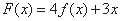 不存在零点;③函数
不存在零点;③函数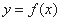 的值域是R;④若函数
的值域是R;④若函数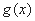 和
和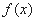 的图像关于原点对称,则函数
的图像关于原点对称,则函数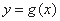 的图像就是方程
的图像就是方程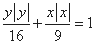 确定的曲线.其中所有正确的命题序号是 ( )
确定的曲线.其中所有正确的命题序号是 ( )
A.①② B.②③ C.①③④ D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=cos x(sin x+cos x)-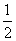 .
.
(1)若0<α<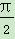 ,且sin α=
,且sin α=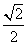 ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高度是46 m,则河流的宽度BC约等于________m.(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,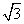 ≈1.73)
≈1.73)
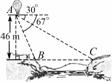 图13
图13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com