解:(1)因为直线x+y+m=0斜率为-1,所以?m∈R直线x+y+m=0都不是y=f(x)的切线等价于f'(x)=3x
2-3a=-1在R上无实数解,所以3a-1<0,所以a的取值范围为
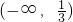
…(4分)
(2)∵f'(x)=3x
2-3a,且f(x)为奇函数,
①当a≤0时,f'(x)≥0恒成立,f(x)在[-1,1]上单调递增,又g(x)=|f(x)|为偶函数,
∴g(x)=|f(x)|在[-1,0]上单调递减,在[0,1]上递增,
∴g(x)的最大值F(a)=g(±1)=|f(±1)|=|1-3a|=1-3a…(6分)
②若a>0,则f'(x)=3x
2-3a=0有两个不同的实数根,且f(x)分别在
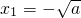
和
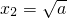
处取得最大值和最小值.
因g(x)=|f(x)|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值
1°若a≥1时,
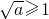
,函数g(x)在[0,1]上单调递增,此时F(a)=g(1)=|1-3a|=3a-1…(8分)
2°若

时,
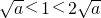
,此时对?x∈[0,1]都有
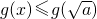
,
∴
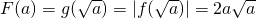
…(10分)
3°若
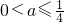
时,
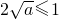
,函数g(x)在x=1处取得最大值,
∴F(a)=g(1)=|f(1)|=|1-3a|=1-3a…(12分)
综上所述
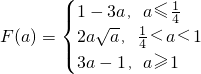
…(14分)
分析:(1)因为直线x+y+m=0斜率为-1,所以?m∈R直线x+y+m=0都不是y=f(x)的切线等价于f'(x)=3x
2-3a=-1在R上无实数解,由此可求a的取值范围;
(2)f'(x)=3x
2-3a,且f(x)为奇函数,分类讨论:①当a≤0时,可得g(x)=|f(x)|在[-1,0]上单调递减,在[0,1]上递增;②若a>0,f(x)分别在
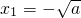
和
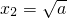
处取得最大值和最小值,因g(x)=|f(x)|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值,由此可得分段函数g(x)的最大值F(a)的解析式.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的最值,考查分类讨论的数学思想,属于中档题.

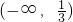 …(4分)
…(4分)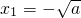 和
和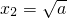 处取得最大值和最小值.
处取得最大值和最小值.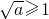 ,函数g(x)在[0,1]上单调递增,此时F(a)=g(1)=|1-3a|=3a-1…(8分)
,函数g(x)在[0,1]上单调递增,此时F(a)=g(1)=|1-3a|=3a-1…(8分) 时,
时,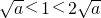 ,此时对?x∈[0,1]都有
,此时对?x∈[0,1]都有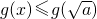 ,
,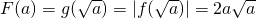 …(10分)
…(10分)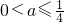 时,
时,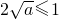 ,函数g(x)在x=1处取得最大值,
,函数g(x)在x=1处取得最大值,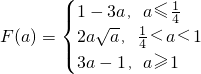 …(14分)
…(14分)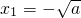 和
和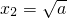 处取得最大值和最小值,因g(x)=|f(x)|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值,由此可得分段函数g(x)的最大值F(a)的解析式.
处取得最大值和最小值,因g(x)=|f(x)|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值,由此可得分段函数g(x)的最大值F(a)的解析式.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<