解:(1)f′(x)=e
x+a,
①当a≥0时,f′(x)≥0,所以f(x)的单调增区间是(-∞,+∞);
②当a<0时,令f′(x)=e
x+a=0,得x=ln(-a),且当x∈(-∞,ln(-a))时,f′(x)<0,当x∈(ln(-a),+∞)时,f′(x)>0,
所以f(x)的单调减区间是(-∞,ln(-a)),单调增区间是(ln(-a),+∞).
(2)因为M∩P=M,所以M⊆P,从而f(x)<x在[

,2]上恒成立.
由e
x+ax<x,得a<1-
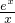
在[

,2]上恒成立.
令h(x)=1-
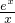
,x∈[

,2],则h′(x)=
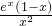
,
所以h(x)在[

,2]上递增,在[1,2]上递减.
又h(

)=1-2

,h(2)=1-
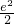
,且h(2)<h(

),所以h
min(x)=h(2)=1-
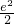
,所以a<1-
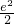
.
所以a的取值范围是(-∞,1-
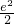
).
(3)由y=g(x)-f(x)=e
xlnx-e
x+x,所以y′=e
x(lnx+

-1)+1.
假设存在x
0∈(0,+∞),使曲线C:y=g(x)-f(x)在点x
0处的切线斜率与f(x)在R上的最小值相等,
由(1)知,当a=-1时,f(x)的最小值是-(-1)+(-1)ln1=1,所以x
0为方程y′=1,即e
x(lnx+

-1)=0的解.
令t(x)=lnx+

-1,x∈(0,+∞),由t′(x)=

-

=

,
知t(x)在(0,1)上为减函数,在(1,+∞)上为增函数,所以t(x)≥t(1)=0,
故方程lnx+

-1=0在(0,+∞)上有唯一解为1.
所以,存在符合条件的x
0,且只有1个.
分析:(1)求出f′(x),解不等式f′(x)>0,f′(x)<0,即得函数的单调区间,注意要对a分类讨论;
(2)由M∩P=M,可得M⊆P,所以问题转化为f(x)<x在[

,2]上恒成立,进而转化为求函数的最值问题解决;
(3)当a=-1时,求出f(x)在R上的最小值,假设存在符合条件的x
0,则x
0为方程y′=f
min(x)的解,构造函数,转化为函数的零点问题,利用导数可以解决.
点评:本题考查应用导数研究函数的单调性、最值问题,关于不等式恒成立问题,往往转化为函数最值问题,方程的解转化为函数零点问题,本题渗透了函数与方程思想及转化思想.

 ≤x≤2}且M∩P=M,求实数a的取值范围;
≤x≤2}且M∩P=M,求实数a的取值范围; ,2]上恒成立.
,2]上恒成立.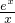 在[
在[ ,2]上恒成立.
,2]上恒成立.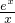 ,x∈[
,x∈[ ,2],则h′(x)=
,2],则h′(x)=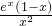 ,
, ,2]上递增,在[1,2]上递减.
,2]上递增,在[1,2]上递减. )=1-2
)=1-2 ,h(2)=1-
,h(2)=1-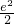 ,且h(2)<h(
,且h(2)<h( ),所以hmin(x)=h(2)=1-
),所以hmin(x)=h(2)=1-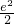 ,所以a<1-
,所以a<1-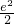 .
.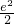 ).
). -1)+1.
-1)+1. -1)=0的解.
-1)=0的解. -1,x∈(0,+∞),由t′(x)=
-1,x∈(0,+∞),由t′(x)= -
- =
= ,
, -1=0在(0,+∞)上有唯一解为1.
-1=0在(0,+∞)上有唯一解为1. ,2]上恒成立,进而转化为求函数的最值问题解决;
,2]上恒成立,进而转化为求函数的最值问题解决;
