
 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.分析 (1)运用离心率公式和准线方程,可得a,c的方程,解得a,c,再由a,b,c的关系,可得b,进而得到椭圆方程;
(2)讨论直线AB的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和弦长公式,以及两直线垂直的条件和中点坐标公式,即可得到所求直线的方程.
解答 解:(1)由题意可得,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
且c+$\frac{{a}^{2}}{c}$=3,解得c=1,a=$\sqrt{2}$,
则b=1,即有椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)当AB⊥x轴,AB=$\sqrt{2}$,CP=3,不合题意;
当AB与x轴不垂直,设直线AB:y=k(x-1),A(x1,y1),B(x2,y2),
将AB方程代入椭圆方程可得(1+2k2)x2-4k2x+2(k2-1)=0,
则x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2({k}^{2}-1)}{1+2{k}^{2}}$,
则C($\frac{2{k}^{2}}{1+2{k}^{2}}$,$\frac{-k}{1+2{k}^{2}}$),且|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$,
若k=0,则AB的垂直平分线为y轴,与左准线平行,不合题意;
则k≠0,故PC:y+$\frac{k}{1+2{k}^{2}}$=-$\frac{1}{k}$(x-$\frac{2{k}^{2}}{1+2{k}^{2}}$),P(-2,$\frac{2+5{k}^{2}}{k(1+2{k}^{2})}$),
从而|PC|=$\frac{2(3{k}^{2}+1)\sqrt{1+{k}^{2}}}{|k|(1+2{k}^{2})}$,
由|PC|=2|AB|,可得$\frac{2(3{k}^{2}+1)\sqrt{1+{k}^{2}}}{|k|(1+2{k}^{2})}$=$\frac{4\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$,解得k=±1,
此时AB的方程为y=x-1或y=-x+1.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理和弦长公式,同时考查两直线垂直和中点坐标公式的运用,属于中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
 在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm.
在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sin2x)=sinx | B. | f(sin2x)=x2+x | C. | f(x2+1)=|x+1| | D. | f(x2+2x)=|x+1| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
已知 ,那么数列
,那么数列 是( )
是( )
A.递减数列 B.递增数列
C.常数列 D.摆动数列
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
已知函数 的图象上存在两点关于
的图象上存在两点关于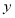 轴对称,则实数
轴对称,则实数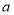 的取值范围是( )
的取值范围是( )
A.[-3,1] B.(-3,1)
C.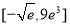 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com