
分析 (Ⅰ)根据顶点在第一象限和顶点在第三象限两种情况分类讨论,求出结果.
(Ⅱ)第k+1项的二项式系数为Cnk,由题意可得关于n的方程,求出n.而二项式系数最大的项为中间项,n为奇数时,中间两项二项式系数相等;n为偶数时,中间只有一项.
解答 解:(Ⅰ)抛物线经过原点,得c=0,
当顶点在第一象限时,a<0,-$\frac{b}{2a}$>0,
即$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$,则有3×4=12(种);
当顶点在第三象限时,a>0,-$\frac{b}{2a}$<0,
即a>0,b>0,则有4×3=12(种);
共计有12+12=24(种).
(Ⅱ)∵Cn4+Cn6=2Cn5,
∴n2-21n+98=0,
∴n=7或n=14.
当n=7时,展开式中二项式系数最大的项是T4和T5,
∴T4的系数=C73($\frac{1}{2}$)423=$\frac{35}{2}$,
T5的系数=C74($\frac{1}{2}$)324=70.
当n=14时,展开式中二项式系数最大的项是T8.
∴T8的系数=C147($\frac{1}{2}$)727=3432.
点评 本题考查满足条件的抛2的条数的求法,考查二项展开式中二项式系数和与系数和问题,难度较大,易出错.要正确区分这两个概念.


科目:高中数学 来源: 题型:选择题
| A. | 奇函数且图象关于直线x=$\frac{π}{2}$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于($\frac{π}{2}$,0)对称 | D. | 偶函数且图象关于点($\frac{π}{2}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
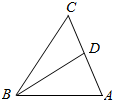 如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.
如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
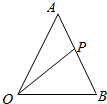 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com