
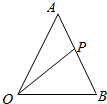
 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.分析 (Ⅰ)根据向量的加减的几何意义,即可求出;
(Ⅱ)根据向量的加减的几何意义,得到$\overrightarrow{OP}•\overrightarrow{AB}$=3-$\frac{13}{1+λ}$,即可求出$\overrightarrow{OP}$•$\overrightarrow{AB}$的取值范围.
解答 解:(Ⅰ)∵λ=$\frac{1}{2}$,
则$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{PB}$,
∴$\overrightarrow{OP}$-$\overrightarrow{OA}$=$\frac{1}{2}$($\overrightarrow{OB}$-$\overrightarrow{OP}$),
∴$\frac{3}{2}$$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$,
则$\overrightarrow{OP}$=$\frac{2}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$,
(Ⅱ)∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|cos60°=6,$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,
∴$\overrightarrow{OP}$-$\overrightarrow{OA}$=λ($\overrightarrow{OB}$-$\overrightarrow{OP}$),(1+λ)$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ$\overrightarrow{OB}$,
∴$\overrightarrow{OP}$=$\frac{1}{1+λ}$$\overrightarrow{OA}$+$\frac{λ}{1+λ}$$\overrightarrow{OB}$,
∴$\overrightarrow{OP}•\overrightarrow{AB}$=($\frac{1}{1+λ}$$\overrightarrow{OA}$+$\frac{λ}{1+λ}$$\overrightarrow{OB}$)($\overrightarrow{OB}$-$\overrightarrow{OA}$)=-$\frac{1}{1+λ}$$\overrightarrow{OA}$2+$\frac{λ}{1+λ}$$\overrightarrow{OB}$2+($\frac{1}{1+λ}$-$\frac{λ}{1+λ}$)$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{-16+9λ+6-6λ}{1+λ}$=$\frac{3λ-10}{1+λ}$=3-$\frac{13}{1+λ}$
∵λ>0,
∴3-$\frac{13}{1+λ}$∈(-10,3),
∴$\overrightarrow{OP}$•$\overrightarrow{AB}$的取值范围为(-10,3).
点评 本题考点是向量在几何中的应用,综合考查了向量三角形法则,向量的线性运算,向量的数量积的运算及数量积公式,熟练掌握向量的相关公式是解题的关键,本题是向量基本题,计算题


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:选择题
 在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{5\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{1}{4}$个单位 | B. | 向右平移$\frac{1}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com