
 ,
, .
. 为
为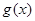 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数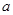 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值. 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:不详 题型:解答题
 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点 在圆弧上,点
在圆弧上,点 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为
 .
.
 关于
关于 的函数关系式?
的函数关系式? 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则
,则 是函数
是函数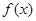 的极值点,因为函数
的极值点,因为函数 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数 的极值点.你认为以上推理的 ( )
的极值点.你认为以上推理的 ( )| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com