
已知函数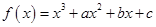 ,曲线
,曲线 在点
在点 处的切线是
处的切线是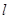 :
:
(Ⅰ)求 ,
,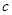 的值;
的值;
(Ⅱ)若 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围
(Ⅰ) 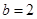 ,
,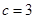 ;(Ⅱ)
;(Ⅱ)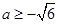
解析试题分析:(Ⅰ)先求出已知函数的导函数,根据切线方程就可以知道曲线在 的函数值和切线斜率,代入函数以及其导函数的解析式求解;(Ⅱ)先由(Ⅰ)得到函数及其导函数的只含有一个参数
的函数值和切线斜率,代入函数以及其导函数的解析式求解;(Ⅱ)先由(Ⅰ)得到函数及其导函数的只含有一个参数 的解析式,然后根据导数与函数单调性的关系将问题转化为
的解析式,然后根据导数与函数单调性的关系将问题转化为 在
在 上的恒成立问题,进行分类讨论解不等式即可
上的恒成立问题,进行分类讨论解不等式即可
试题解析:解:(Ⅰ) 由已知得 , 2分
, 2分
因为曲线 在点
在点 处的切线是
处的切线是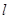 :
: ,
,
所以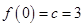 ,
, ,即
,即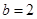 ,
,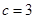 6分
6分
(Ⅱ)由(Ⅰ)知 ,
, ,
,
因为 在
在 上单调递增,所以
上单调递增,所以 在
在 上恒成立 8分
上恒成立 8分
当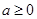 时,
时, 在
在 上单调递增,
上单调递增,
又因为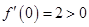 ,所以
,所以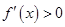 在
在 上恒成立 10分
上恒成立 10分
当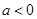 时,要使得
时,要使得 在
在 上恒成立,那么
上恒成立,那么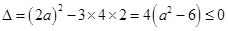 ,
,
解得 12分
12分
综上可知,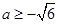 14分
14分
考点:1、利用导数研究函数的切线方程;2、函数的单调性与导数的关系3、分类讨论思想


科目:高中数学 来源: 题型:解答题
已知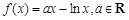 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在
在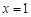 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(3)是否存在实数 ,使
,使 在区间
在区间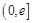 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数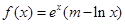 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数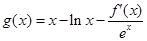 的最小值为1,其中
的最小值为1,其中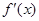 是函数f(x)的导数.
是函数f(x)的导数.
(1)求m的值.
(2)判断直线y=e是否为曲线f(x)的切线,若是,试求出切点坐标和函数f(x)的单调区间;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖北宜昌“三峡人家”风景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值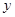 万元与投入
万元与投入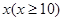 万元之间满足:
万元之间满足: ,
, 为常数,当
为常数,当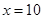 万元时,
万元时, 万元;当
万元;当 万元时,
万元时, 万元.(参考数据:
万元.(参考数据: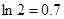 ,
, ,
, )
)
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求该景点改造升级后旅游利润 的最大值.(利润=旅游收入-投入)
的最大值.(利润=旅游收入-投入)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分共12分)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2
(Ⅰ)求a,b,c,d的值
(Ⅱ)若x≥-2时,f(x)≤kg(x),求k的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, 为函数
为函数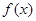 的导函数.
的导函数.
(1)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是 ,求
,求 的值;
的值;
(2)若函数 ,求函数
,求函数 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( 是自然对数的底数).
是自然对数的底数).
(1)若曲线 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值;
(2)当 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与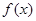 在
在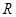 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com