考点:数列与不等式的综合,数列的求和
专题:计算题,等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)将a
1=1,a
2=2代入a
1+2a
2+…+na
n=n(n+1)b
n求b
1,b
2;
(Ⅱ)由a
n=
可得na
n=n+1,由a
1+2a
2+…+na
n=n(n+1)b
n可得b
n=
,从而证明b
n>
;
(Ⅲ)由b
n=n
2代入a
1+2a
2+…+na
n=n(n+1)b
n,从而求数列{a
n}的通项公式.
解答:
解:(Ⅰ)当n=1时,有a
1=2b
1=1,
则b
1=
,
当n=2时,有a
1+2a
2=2×(2+1)b
2,
又∵a
1=1,a
2=2,
∴b
2=
.
(Ⅱ)∵a
n=
,
∴na
n=n•
=n+1,
∴a
1+2a
2+…+na
n=
=n(n+1)b
n,
∴b
n=
=
(1+
)
>.
(Ⅲ)当n>1时,
∵a
1+2a
2+…+na
n=n(n+1)b
n,①
∴a
1+2a
2+…+(n-1)a
n-1=n(n-1)b
n-1,②
①-②得,
na
n=n(n+1)b
n-n(n-1)b
n-1,
即a
n=(n+1)b
n-(n-1)b
n-1,
又∵b
n=n
2,
∴a
n=(n+1)n
2-(n-1)(n-1)
2=4n
2-3n+1,(n≥2).
当n=1时,b
1=1
2,又a
1=2b
1=2也符合上式.
∴a
n=4n
2-3n+1 (n∈N
+).
点评:本题考查了数列的化简与求和,同时考查了整体代换的方法,化简比较复杂,属于难题.



 阅读快车系列答案
阅读快车系列答案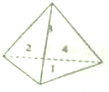 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.