设函数f(x)=x(lnx+a)-ax2,其中a∈R.
(1)若a=0,求f(x)的单调区间及极值;
(2)当x≥1时,f(x)≤0,求a的取值范围.
解:(1)当a=0时,f(x)=xlnx
∴f'(x)=lnx+1,x∈(0,+∞)
又∵当x∈(0,

)时,f'(x)<0,
当x∈(

,+∞)时,f'(x)>0,
∴f(x)在(0,

)上单调递减,在(

,+∞)上单调递增,在x=

处取得极大值,且极大值为f(

)=-

(2)当x≥1时,f(x)≤0?lnx+a-ax≤0.
令g(x)=lnx+a-ax,则

.
①当a≥1时,g'(x)≤0,故g(x)
在[1,+∞)是减函数,所以g(x)≤g(1)=0.
②当0<a<1时,令g'(x)=0,得
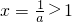
.
∵当
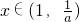
时,g'(x)>0,
故当
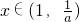
时,g(x)>g(1)=0,与题意不符.
③当a≤0时,g'(x)>0,故g(x)在[1,+∞)是增函数,从而当x∈(1,+∞)时,
有g(x)>g(1)=0,与题意不符.综上所述,a的取值范围为[1,+∞).
分析:(1)由原函数的解析式,我们易求出函数的导函数,进而根据导函数的零点对函数的定义域进行分段讨论后,即可得到答案.
(2)若f(x)≤0,即x(lnx+a)-ax
2≤0,对a进行分类讨论后,综合即可得到答案.
点评:本题考查的知识点是利用导数研究函数的单调性,及函数的单调性与导数的关系,其中根据已知条件求出导函数是解答本题的关键.

 )时,f'(x)<0,
)时,f'(x)<0, ,+∞)时,f'(x)>0,
,+∞)时,f'(x)>0, )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增,在x=
,+∞)上单调递增,在x= 处取得极大值,且极大值为f(
处取得极大值,且极大值为f( )=-
)=-
 .
.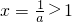 .
.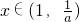 时,g'(x)>0,
时,g'(x)>0,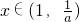 时,g(x)>g(1)=0,与题意不符.
时,g(x)>g(1)=0,与题意不符.

 备战中考寒假系列答案
备战中考寒假系列答案