
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合进行求解即可.
解答 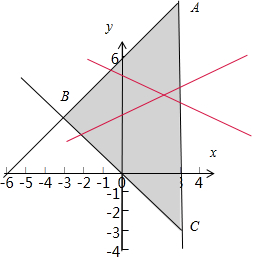 解:由z=ax+y得y=-ax+z,直线y=-ax+z是斜率为-a,y轴上的截距为z的直线,
解:由z=ax+y得y=-ax+z,直线y=-ax+z是斜率为-a,y轴上的截距为z的直线,
作出不等式组$\left\{\begin{array}{l}{x≤3}\\{x+y≥0}\\{x-y+6≥0}\end{array}\right.$对应的平面区域如图:
则A(3,9),B(-3,3),C(3,-3),
∵z=ax+y的最大值为3a+9,最小值为3a-3,
可知目标函数经过A取得最大值,经过C取得最小值,
若a=0,则y=z,此时z=ax+y经过A取得最大值,经过C取得最小值,满足条件,
若a>0,则目标函数斜率k=-a<0,
要使目标函数在A处取得最大值,在C处取得最小值,
则目标函数的斜率满足-a≥kBC=-1,
即a≤1,可得a∈(0,1].
若a<0,则目标函数斜率k=-a>0,
要使目标函数在A处取得最大值,在C处取得最小值,可得-a≤kBA=1
∴-1≤a<0,综上a∈[-1,1]
故答案为:[-1,1].
点评 本题主要考查线性规划的应用,根据条件确定A,B是最优解是解决本题的关键.注意要进行分类讨论,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | {x|x2≤1} | C. | (1,2) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
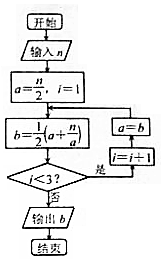 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n=12,则输出的结果b=( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n=12,则输出的结果b=( )| A. | 4 | B. | $\frac{7}{2}$ | C. | $\frac{97}{28}$ | D. | $\frac{64}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | [-1,1] | C. | (0,1] | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1+ln2}{2}$,-$\frac{1+ln3}{3}$) | B. | [$\frac{1+ln3}{3}$,$\frac{1+ln2}{2}$) | C. | (-$\frac{1+ln2}{2}$,-$\frac{1+ln3}{3}$] | D. | (-1,-$\frac{1+ln3}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{4}$,0) | B. | (-∞,-$\frac{3}{4}$) | C. | (-3,-$\frac{3}{4}$) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com