
(本题满分16分)数列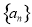 ,
,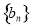 ,
,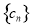 满足:
满足: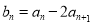 ,
,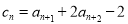 ,
,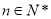 .
.
(1)若数列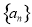 是等差数列,求证:数列
是等差数列,求证:数列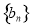 是等差数列;
是等差数列;
(2)若数列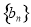 ,
,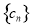 都是等差数列,求证:数列
都是等差数列,求证:数列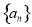 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列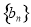 是等差数列,试判断当
是等差数列,试判断当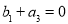 时,数列
时,数列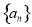 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
(1)详见解析(2)详见解析(3)数列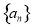 成等差数列.
成等差数列.
【解析】
试题分析:(1)证明一个数列为等差数列,一般从等差数列定义出发: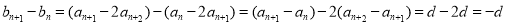 ,其中
,其中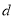 为等差数列
为等差数列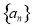 的公差(2)同(1),先根据关系式
的公差(2)同(1),先根据关系式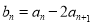 ,
,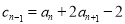 解出
解出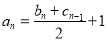 ,再从等差数列定义出发
,再从等差数列定义出发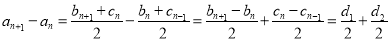 ,其中
,其中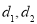 分别为等差数列
分别为等差数列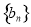 ,
,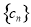 的公差(3)探究性问题,可将条件向目标转化,一方面
的公差(3)探究性问题,可将条件向目标转化,一方面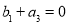 ,所以
,所以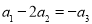 ,即
,即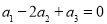 ,另一方面
,另一方面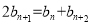 ,所以
,所以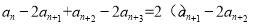 ,整理得
,整理得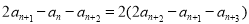 ,从而
,从而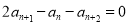 ,即数列
,即数列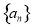 成等差数列.
成等差数列.
试题解析:证明:(1)设数列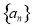 的公差为
的公差为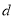 ,
,
∵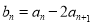 ,
,
∴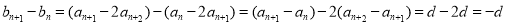 ,
,
∴数列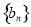 是公差为
是公差为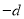 的等差数列. 4分
的等差数列. 4分
(2)当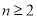 时,
时,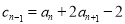 ,
,
∵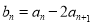 ,∴
,∴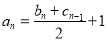 ,∴
,∴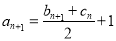 ,
,
∴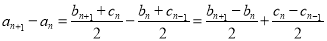 ,
,
∵数列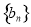 ,
,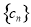 都是等差数列,∴
都是等差数列,∴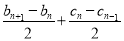 为常数,
为常数,
∴数列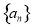 从第二项起为等差数列. 10分
从第二项起为等差数列. 10分
(3)数列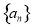 成等差数列.
成等差数列.
解法1 设数列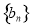 的公差为
的公差为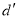 ,
,
∵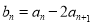 ,
,
∴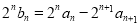 ,∴
,∴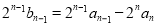 , ,
, ,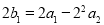 ,
,
∴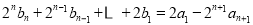 ,
,
设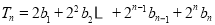 ,∴
,∴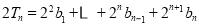 ,
,
两式相减得: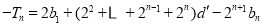 ,
,
即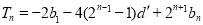 ,∴
,∴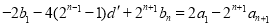 ,
,
∴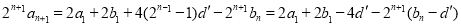 ,
,
∴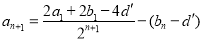 , 12分
, 12分
令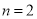 ,得
,得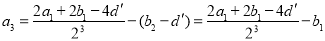 ,
,
∵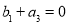 ,∴
,∴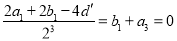 ,∴
,∴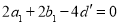 ,
,
∴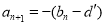 ,∴
,∴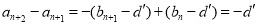 ,
,
∴数列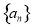 (
(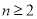 )是公差为
)是公差为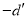 的等差数列, 14分
的等差数列, 14分
∵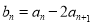 ,令
,令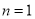 ,
,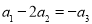 ,即
,即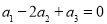 ,
,
∴数列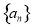 是公差为
是公差为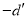 的等差数列. 16分
的等差数列. 16分
解法2 ∵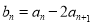 ,
,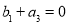 ,
,
令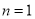 ,
,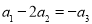 ,即
,即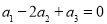 , 12分
, 12分
∴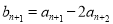 ,
,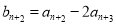 ,
,
∴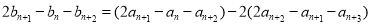 ,
,
∵数列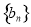 是等差数列,∴
是等差数列,∴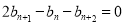 ,
,
∴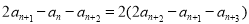 , 14分
, 14分
∵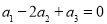 ,∴
,∴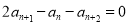 ,
,
∴数列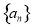 是等差数列. 16分
是等差数列. 16分
考点:等差数列定义
考点分析: 考点1:等差数列 试题属性

科目:高中数学 来源: 题型:
函数y=f(x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在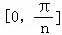 上的面积为
上的面积为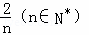 ,则函数y=sin(3x﹣π)+1在
,则函数y=sin(3x﹣π)+1在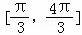 上的面积为.
上的面积为.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末理科数学试卷(解析版) 题型:填空题
已知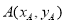 是单位圆上任一点,将射线OA绕点O逆时针旋转
是单位圆上任一点,将射线OA绕点O逆时针旋转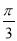 到OB交单位圆于点
到OB交单位圆于点 ,已知
,已知 若
若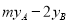 的最大值为3,则
的最大值为3,则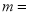

查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末理科数学试卷(解析版) 题型:填空题
在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试文科数学试卷(解析版) 题型:填空题
在梯形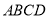 中,
中,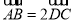 ,
,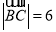 ,
,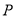 为梯形
为梯形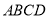 所在平面上一点,且满足
所在平面上一点,且满足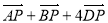 =0,
=0,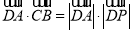 ,
,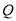 为边
为边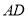 上的一个动点,则
上的一个动点,则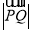 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试文科数学试卷(解析版) 题型:填空题
袋子里有两个不同的红球和两个不同的白球,从中任取两个球,则这两个球颜色相同的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分14分)
如图,在多面体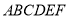 中,四边形
中,四边形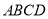 是菱形,
是菱形,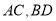 相交于点
相交于点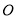 ,
,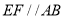 ,
,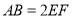 ,平面
,平面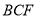
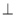 平面
平面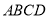 ,
,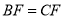 ,点
,点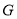 为
为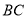 的中点.
的中点.

(1)求证:直线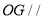 平面
平面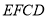 ;
;
(2)求证:直线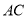
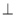 平面
平面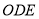 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试文科数学试卷(解析版) 题型:解答题
(本小题满分14分)在△ABC中,角A,B,C的对边分别为a,b,c.已知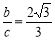 ,
,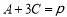 .
.
(1)求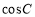 的值;(2)求
的值;(2)求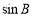 的值;(3)若
的值;(3)若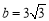 ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com