函数y=f（x）的图象与直线x=a，x=b及x轴所围成图形的面积称为函数f（x）在[a，b]上的面积，已知函数y=sinnx在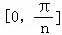
上的面积为
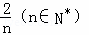，则函数y=sin（3x﹣π）+1在
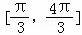上的面积为．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
下列向量中，可以作为基底的是（）
A． 
=（0，0），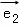
=（1，﹣2） B． 
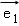=（2，﹣3），=（﹣
，
）
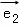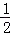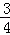C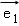． =（3，5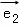），=（6，10） D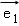． =（1，﹣2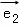），=（5，7）
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=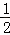
（|x﹣a2|+|x﹣2a2|﹣3a2），若∀x∈R，f（x﹣1）≤f（x），则实数a的取值范围为（）
A． [﹣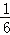
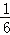，] B． [﹣
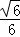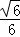，] C． [﹣
，
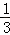] D． [﹣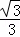
，]
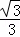查看答案和解析>>
科目：高中数学 来源： 题型：
设函数f（x）=ax﹣（k﹣1）a﹣x（a＞0且a≠1）是定义域为R的奇函数．
（1）若f（1）＞0，试判断函数f（x）的单调性，并求使不等式f（sin2θ+cos2θ）+f（1﹣tcosθ）＜0对所有的θ∈（0，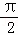
）均成立的t的取值范围；
（2）若f（1）=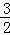
，g（x）=a2x+a﹣2x﹣2mf（x），且g（x）在[1，+∞）上的最小值为﹣1，求m的值．
查看答案和解析>>
科目：高中数学 来源：2014-2015学年江苏省泰州市高三上学期期末考试文科数学试卷（解析版） 题型：解答题
（本题满分16分）数列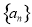
，
，
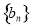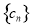满足：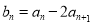
，
，
．
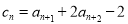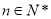（1）若数列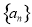是等差数列，求证：数列
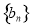是等差数列；
（2）若数列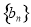
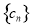，都是等差数列，求证：数列
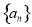从第二项起为等差数列；
（3）若数列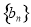是等差数列，试判断当
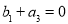时，数列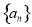是否成等差数列？证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
解：对于函数y=sin3x而言，n=3，
]上的面积为：
，
上的面积为
，
，
满足
，且
.
的解析式；
恒成立，求实数m的取值范围.
_____________
上的值域为 （ ）
B. 
C. 
D.
的展开式中含有
项，则n的最小值为 【 】