
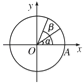
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.
【答案】α=(![]() )°,β=(
)°,β=(![]() )°.
)°.
【解析】
试题确定α=![]() 180°,β=
180°,β=![]() 180°,m,n∈Z,利用2α,2β均为钝角,即可得到结论.
180°,m,n∈Z,利用2α,2β均为钝角,即可得到结论.
解:根据题意可知:14α,14β均为360°的整数倍,故可设14α=m360°,m∈Z,14β=n360°,n∈Z,从而可知α=![]() 180°,β=
180°,β=![]() 180°,m,n∈Z.
180°,m,n∈Z.
又由两只蚂蚁在第2秒时均位于第二象限,则2α,2β在第二象限.
又0°<α<β<180°,从而可得0°<2α<2β<360°,
因此2α,2β均为钝角,即90°<2α<2β<180°.
于是45°<α<90°,45°<β<90°.
∴45°<![]() 180°<90°,45°<
180°<90°,45°<![]() 180°<90°,
180°<90°,
即![]() <m<
<m<![]() ,
,![]() <n<
<n<![]() .
.
又∵α<β,∴m<n,从而可得m=2,n=3.
即α=(![]() )°,β=(
)°,β=(![]() )°.
)°.


科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为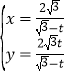 (
(![]() 为参数,且
为参数,且![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并将曲线
的参数方程化为普通方程,并将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求曲线![]() 与曲线
与曲线![]() 交点的极坐标
交点的极坐标![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足: .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 试确定
试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com