
【题目】已知![]() ,
,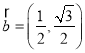 ,函数
,函数![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的实数根
上有两个不同的实数根![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]() (3)
(3)![]() 或
或![]() 或
或![]()
【解析】
(1)由向量数量积的坐标运算及辅助角公式可得![]() ,再解方程
,再解方程![]() 即可;
即可;
(2)原命题可转化为![]() ,
,![]() 恒成立,再求实数
恒成立,再求实数![]() 的取值范围;
的取值范围;
(3)原方程可以化为![]() ,则
,则![]() 或
或![]() ,再讨论
,再讨论![]() 的取值范围使得方程有两个解即可.
的取值范围使得方程有两个解即可.
解:(1)由![]() ,
,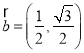 ,
,
又![]() ,则
,则![]() ,
,
即![]() ,
,
又因为![]() ,则
,则![]() ,或
,或![]() ,
,
则![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() .
.
(2)当![]() 时,
时,![]() ,可得
,可得![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() 恒成立,
恒成立,
则 可得
可得![]() .
.
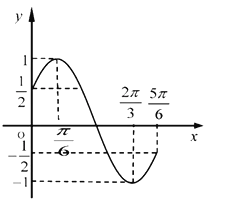
(3)可知函数![]() 在区间
在区间![]() 和
和![]() 上为增函数,在
上为增函数,在![]() 上为减函数,画出函数
上为减函数,画出函数![]() 在
在![]() 上的图象.
上的图象.
原方程可以化为![]() ,则
,则![]() 或
或![]() ,
,
①当![]() 时,则
时,则![]() ,要使得原方程有两个不同的实数解,只需
,要使得原方程有两个不同的实数解,只需![]() ,即
,即![]() ,
,
②当![]() 时,则
时,则![]() ,可知原方程的根为
,可知原方程的根为![]() ,
,![]() ;
;
③当![]() 时,则
时,则![]() ,可知原方程有3个根,不符合题意;
,可知原方程有3个根,不符合题意;
④当![]() 时,
时,![]() ,可知原方程的根为
,可知原方程的根为![]() ,
,![]() ;
;
⑤当![]() 时,则
时,则![]() ,可知原方程有3个根,不符合题意.
,可知原方程有3个根,不符合题意.
综上可知,当![]() 或
或![]() 或
或![]() 时,原方程有两个不同的根.
时,原方程有两个不同的根.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数x,满足
,若在定义域内存在实数x,满足![]() ,其中k为整数,则称函数
,其中k为整数,则称函数![]() 为定义域上的“k阶局部奇函数”.
为定义域上的“k阶局部奇函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为
是否为![]() 上的“2阶局部奇函数”?并说明理由;
上的“2阶局部奇函数”?并说明理由;
(2)若![]() 是
是![]() 上的“1阶局部奇函数”,求实数m的取值范围;
上的“1阶局部奇函数”,求实数m的取值范围;
(3)若![]() ,对任意的实数
,对任意的实数![]() ,函数
,函数![]() 恒为
恒为![]() 上的“k阶局部奇函数”,求整数k取值的集合.
上的“k阶局部奇函数”,求整数k取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+6|﹣|m﹣x|(m∈R)
(1)当m=3时,求不等式f(x)≥5的解集;
(2)若不等式f(x)≤7对任意实数x恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沃尔玛超市委托某机构调查该超市的顾客使用移动支付的情况.调查人员从年龄在![]() 内的顾客中,随机抽取了200人,调查结果如图所示:
内的顾客中,随机抽取了200人,调查结果如图所示:

(1)为推广移动支付,超市准备对使用移动支付的每位顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关.
的把握认为使用移动支付与年龄有关.
|
| 总计 | |
使用移动支付 | |||
不使用移动支付 | |||
总计 |
 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 | /tr>
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校“统计”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表,为了判断主修统计专业是否与性别有关,计算得到![]() ,因为
,因为![]() ,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
专业 性别 | 非统计专业 | 统计专业 |
男 | 13 | 10 |
女 | 7 | 20 |
本题可以参考独立性检验临界值表:
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】安庆市某中学教研室从高二年级随机抽取了![]() 名学生的十月份语文成绩(满分
名学生的十月份语文成绩(满分![]() 分,成绩均为不低于
分,成绩均为不低于![]() 分的整数),得到如图所示的频率分布直方图.
分的整数),得到如图所示的频率分布直方图.

(1)若该校高二年级共有学生![]() 人,试估计十月份月考语文成绩不低于
人,试估计十月份月考语文成绩不低于![]() 分的人数;
分的人数;
(2)为提高学生学习语文的兴趣,学校决定在随机抽取的![]() 名学生中成立“二帮一”小组,即从成绩
名学生中成立“二帮一”小组,即从成绩![]() 中选两位同学,共同帮助
中选两位同学,共同帮助![]() 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为![]() 分,乙同学的成绩为
分,乙同学的成绩为![]() 分,求甲乙恰好被安排在同一小组的概率.
分,求甲乙恰好被安排在同一小组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com