
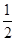 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.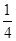 (Ⅱ)
(Ⅱ)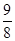
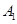 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”,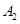 表示事件“第3局甲参加比赛时,结果为甲负”,
表示事件“第3局甲参加比赛时,结果为甲负”,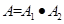 . 3分
. 3分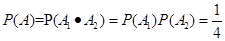 . 6分
. 6分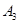 表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
表示事件“第3局乙和丙比赛时,结果为乙胜丙”,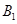 表示事件“第1局结果为乙胜丙”,
表示事件“第1局结果为乙胜丙”,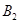 表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
表示事件“第2局乙和甲比赛时,结果为乙胜甲”,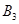 表示事件“第3局乙参加比赛时,结果为乙负”.
表示事件“第3局乙参加比赛时,结果为乙负”.
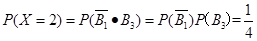 ,
,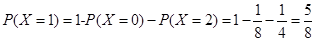 , 10分
, 10分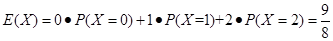 . 12分
. 12分 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”,  表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即
表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即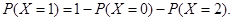


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 序号i | 分组(睡眠时间) | 组中值(Gi) | 频数(人数) | 频率(Fi) |
| 1 | [4,5) | 4.5 | 6 | 0.12 |
| 2 | [5,6) | 5.5 | 10 | 0.20 |
| 3 | [6,7) | 6.5 | 20 | 0.40 |
| 4 | [7,8) | 7.5 | 10 | 0.20 |
| 5 | [8,9] | 8.5 | 4 | 0.08 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
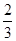 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为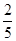 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.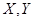 ,求
,求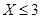 的概率;
的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 相切的概率;
相切的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
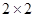 列联表;
列联表;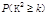 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
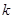 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
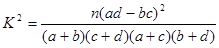 (
(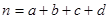 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
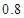 ,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记
,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记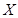 为5个同学的得分总和,则
为5个同学的得分总和,则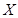 的数学期望为( )
的数学期望为( )| A.400 | B.200 | C.100 | D.80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com