
 相切的概率;
相切的概率; (2)
(2)
 即:a2+b2=25,由于a,b∈{1,2,3,4,5,6}
即:a2+b2=25,由于a,b∈{1,2,3,4,5,6}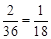
 .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求

 +2的概率。
+2的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、
、 、
、 四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于
四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于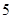 中一等奖,等于
中一等奖,等于 中二等奖,等于
中二等奖,等于 中三等奖。
中三等奖。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
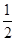 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.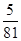 | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
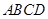 的边长为2,
的边长为2,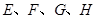 分别是边
分别是边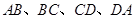 的中点.
的中点.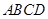 内部随机取一点
内部随机取一点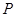 ,求满足
,求满足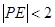 的概率;
的概率;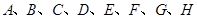 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求
,求 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com