
分析 (1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),运用离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(2)求得椭圆的焦点和左右顶点,可设双曲线的方程$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m,n>0),求得m,n,即可得到双曲线的方程.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得2b=10,e=$\frac{c}{a}$=$\frac{2}{3}$,a2-b2=c2,
解得b=5,a=3$\sqrt{5}$,c=2$\sqrt{5}$,
即有椭圆的方程为$\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1;
(2)设双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m,n>0),
由椭圆的焦点为(±2$\sqrt{5}$,0),可得m=2$\sqrt{5}$,
由椭圆的左右顶点为(±3$\sqrt{5}$,0),
可得$\sqrt{{m}^{2}+{n}^{2}}$=3$\sqrt{5}$,
解得n=5,
即有双曲线的方程为$\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1.
点评 本题考查椭圆和双曲线的方程的求法,注意运用椭圆的离心率公式和双曲线的性质,考查运算能力,属于基础题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
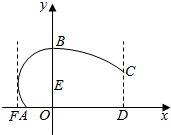 某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).
某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com