
 与时刻
与时刻 (时)的关系为
(时)的关系为 ,
,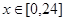 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作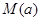 .
. ,
,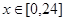 ,求
,求 的取值范围;
的取值范围; 的取值范围是
的取值范围是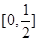 ;(2)当
;(2)当 时,污染指数不超标;当
时,污染指数不超标;当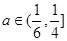 时,污染指数超标.
时,污染指数超标. 的表达式可知,可以考虑利用基本不等式求
的表达式可知,可以考虑利用基本不等式求 的取值范围,首先讨论当当
的取值范围,首先讨论当当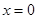 时,
时,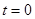 ,而当
,而当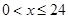 时:
时: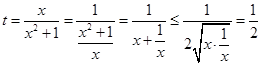 ,
, ,即
,即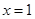 时取等号,而显然
时取等号,而显然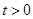 ,因此
,因此 的取值范围是
的取值范围是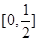 ;(2)根据条件结合(1)分析可知,可将污染指数转化为与
;(2)根据条件结合(1)分析可知,可将污染指数转化为与 有关的函数
有关的函数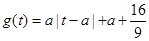 ,利用(1)中求得的
,利用(1)中求得的 的取值范围,可知
的取值范围,可知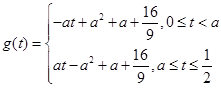 ,显然
,显然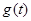 在
在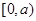 上单调递减,在
上单调递减,在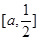 上单调递增,∴
上单调递增,∴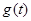 的最大值只可能在
的最大值只可能在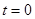 或
或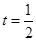 时取到,通过比较可知
时取到,通过比较可知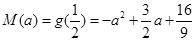 ,从而若市中心的污染指数未超标,则等价于
,从而若市中心的污染指数未超标,则等价于 ,解关于
,解关于 的不等式组
的不等式组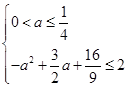 ,从而可以得到相应结论:当
,从而可以得到相应结论:当 时,污染指数不超标;当
时,污染指数不超标;当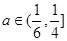 时,污染指数超标.
时,污染指数超标.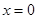 时:
时: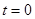 , 1分
, 1分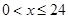 时:
时: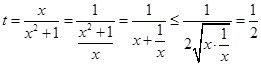 , 4分
, 4分 ,即
,即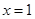 时取等号, 5分 而显然
时取等号, 5分 而显然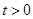 ,
, 的取值范围是
的取值范围是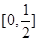 ; 6分
; 6分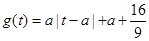 ,
,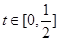 ,则
,则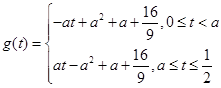 , 8分
, 8分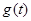 在
在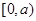 上单调递减,在
上单调递减,在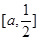 上单调递增,∴
上单调递增,∴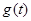 的最大值只可能在
的最大值只可能在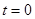 或
或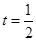 时取到,
时取到,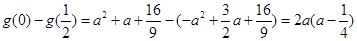 ,∵
,∵ ,∴
,∴ ,
,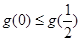 ,∴
,∴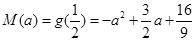 , 11分
, 11分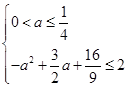 得
得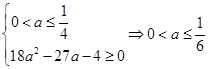 , 13分
, 13分 时,污染指数不超标;当
时,污染指数不超标;当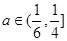 时,污染指数超标. 14分
时,污染指数超标. 14分

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
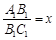 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;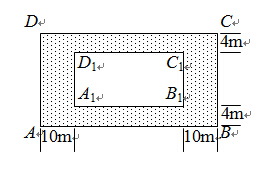
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com