练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求下列函数的定义域：
    （1）y=数学公式+数学公式；
    （2）y=数学公式．

    解：（1）要使函数有意义，
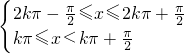
    则即（k∈Z），
    所以2kπ≤x＜2kπ+（k∈Z）．
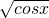
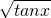
    所以函数y=+的定义域是
    {x|2kπ≤x＜2kπ+，k∈Z}．
    （2）由函数式有意义得
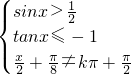
    得（k∈Z）．

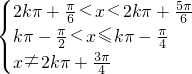
    即（k∈Z）．
    求交集得2kπ+＜x＜2kπ+（k∈Z）．
    所以函数的定义域是{x|2kπ+＜x＜2kπ+，k∈Z}．
    分析：（1）要使函数有意义，则根据负数不能开偶次方根，即由求解．
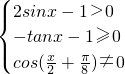
    （2）由函数式有意义，一是真数大于零，二是负不能开偶次方根，三是分母不能为零，即由求解．
    点评：本题主要考查了定义域的常见类型一是对数函数真数大于零，二是负数不能开偶次根，三是分母能为零，涉及到三角不等式的解法，要多借助图象．
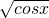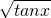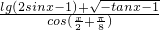    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    求下列函数的定义域（要求用区间表示）：
    （1）f(x)=
    		4-x
    2x-3
    +log3(x+1)    ；         （2）y=
    		1-log2(4x-5)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求下列函数的定义域：
    （1）f(x)=
    		1-(
    1
    2
    )    x
    ；  
    （2）g(x)=
    1
    log3(3x-2)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求下列函数的定义域：
    （1）y=
    		sinx-cosx
    ；       
    （2）y=
    		2+log
    1
    2
    x
    +
    		tanx
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求下列函数的定义域与值域
    （1）y=
    x
    1
    2
    +x-
    1
    2
    x
    1
    2
    -x-
    1
    2
    ；
    （2）y=
    		-(lo
    g
    x
    1
    4
    )    2    +lo
    g
    x
    1
    4
    +2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求下列函数的定义域：
    （1）f（x）=
    1
    x-1

    （2）f（x）=
    		1-(
    1
    2
    )    x
    ．

    查看答案和解析>>

    同步练习册答案