Question

4．如图所示，在梯形ABCD中，∠A=$\frac{π}{2}$，$AB=\sqrt{2}$，BC=2，$AD=\frac{3}{2}$点E为AB的中点，则$\overrightarrow{CE}•\overrightarrow{BD}$=-2．

Answer 1

分析 以B为原点，BC为x轴，AB为y轴建系，求出相关点的坐标，求出向量即可求解数量积．

解答 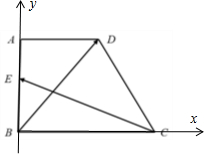解：以B为原点，BC为x轴，AB为y轴建系，C（2，0），$E（{0，\frac{{\sqrt{2}}}{2}}）$，B（0，0），$D=（{\frac{3}{2}，\sqrt{2}}）$，
∴$\overrightarrow{CE}=（{-2，\frac{{\sqrt{2}}}{2}}）$，$\overrightarrow{BD}=（{\frac{3}{2}，\sqrt{2}}）$，所以$\overrightarrow{CE}•\overrightarrow{BD}=-3+1=-2$．
故答案为：-2．

点评 本题考查向量的数量积的应用，考查计算能力．