
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于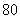 小于
小于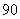 为二等品,小于
为二等品,小于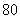 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利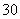 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |
|
|
|
|
|
|
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.
科目:高中数学 来源: 题型:
已知过点A(-4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B,C两点.当直线l的斜率是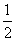 时,
时,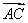 =4
=4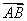 .
.
(1)求抛物线G的方程;
(2)设线段BC的中垂线在y轴上的截距为b,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如右图所示,
求△ABO的面积的最小值及此时直线l的方程.
审题路线 根据截距式设所求直线l的方程⇒把点P代入,找出截距的关系式⇒运用基本不等式求S△ABO⇒运用取等号的条件求出截距⇒得出直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com