
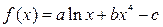 (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值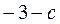 ,其中a,b,c为常数。
,其中a,b,c为常数。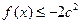 恒成立,求c的取值范围。
恒成立,求c的取值范围。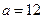 ,
, ;
;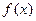 的单调递增区间为
的单调递增区间为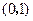 ,而
,而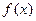 的单调递减区间为
的单调递减区间为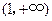 ;
;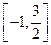
 ,因此
,因此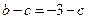 ,从而
,从而 .-------1分
.-------1分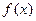 求导得
求导得 . --------------------------------2分
. --------------------------------2分 ,因此
,因此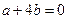 ,解得
,解得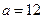 . ---------------------3分
. ---------------------3分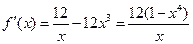 (
( ),令
),令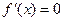 ,解得
,解得 .--5分
.--5分 时,
时,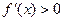 ,此时
,此时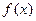 为增函数;
为增函数; 时,
时, ,此时
,此时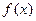 为减函数.--------------------------------7分
为减函数.--------------------------------7分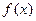 的单调递增区间为
的单调递增区间为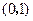 ,而
,而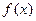 的单调递减区间为
的单调递减区间为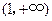 .--------8分
.--------8分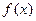 在
在 处取得极大值
处取得极大值 ,此极大值也是最大值,要使
,此极大值也是最大值,要使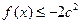 (
( )恒成立,只需
)恒成立,只需 .------------------------10分
.------------------------10分 ,从而
,从而 ,
, .所以
.所以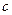 的取值范围为
的取值范围为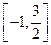 .----------------------------12分
.----------------------------12分

科目:高中数学 来源:不详 题型:解答题
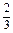 .
.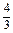 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
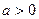 ,函数
,函数 .(1)设曲线
.(1)设曲线 在点
在点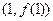 处的切线为
处的切线为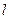 ,若
,若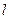 与圆
与圆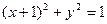 相切,求
相切,求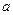 的值;(2)求函数
的值;(2)求函数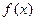 的单调区间;(3)求函数
的单调区间;(3)求函数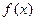 在[0,1]上的最小值。
在[0,1]上的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
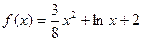 ,
,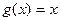 .
.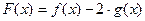 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数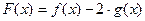 在
在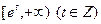 上有零点,求
上有零点,求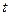 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当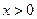 时,有
时,有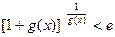 成立;若
成立;若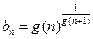 (
(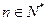 ),试问数列
),试问数列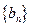 中是否存在
中是否存在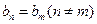 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(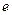 为自然对数的底数)
为自然对数的底数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com