
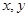 满足约束条件
满足约束条件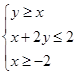 ,则
,则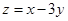 的最小值为( )
的最小值为( )A.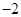 | B.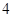 | C.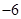 | D.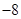 |
科目:高中数学 来源:不详 题型:解答题
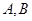 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套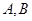 型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套
型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套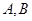 型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产
型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产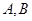 两型会议桌多少套,才能获得最大利润?最大利润是多少?
两型会议桌多少套,才能获得最大利润?最大利润是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com