
分析 (1)根据题意,a1=a5=0,a2=±1,a4=±1,再根据|ak+1-ak|=1求出a3=0,可以得出符合题设的E数列A5;
(2)可先证明必要性:由递增数列的定义,得到An是首项为1,公差为-的等差数列.即可求得a2016=1+(2016-1)×1=2016;再证充分性:由新定义推出a2016≥a1+2015,又因为a1=1,a2016=2016,所以a2016=a1+2015.得证;
(3)由a1=0,|ak+1-ak|=d>0,可得a2=d或-d,然后不适一般性验证即可.
解答 解:(1)∵数列E数列An满足|ak+1-ak|=d>0,
∴满足a1=a5=0的所有E数列A5四个:①0,d,0,d,0;
②0,-d,0,-d,0;③0,-d,0,d,0;④0,d,0,-d,0.
任意写出两个即可,答案不唯一;
(2)证明:必要性:因为F数列A2016是递增数列,
所以ak+1-ak=1(k=1,2,…,2015).
所以An是首项为1,公差为1的等差数列.
所以a2016=1+(2016-1)×)=2016.
充分性:由于a2016-a2015≥1,
a2015-a2014≥1
…
a2-a1≥1
所以a2016-a1≥2015,即a2016≥a1+2015,
又因为a1=1,a2016=2016,
所以a2016=a1+2015.
故an+1-an=1>0(k=1,2,…,2015)即An是递增数列.
综上,结论得证;
(3)由a1=0,|ak+1-ak|=d>0,可得a2=d或-d,
a1=0,a2=d,a3=0,a4=-d,S(An)=0;
a1=0,a2=d,a3=2d,a4=-d,a5=0,a6=-d,a3=-2d,a4=-d,S(An)=0
不适一般性,可得n=4k,k∈N*,S(An)=0.
点评 本题考查数列新定义及理解,考查数列的运用,充分必要条件的证明,解题的关键在于对新定义的正确运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非允分条件 | ||
| C. | 非充分非必要条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
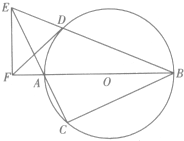 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.求证:
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(-1,0)∪(2,+∞) | B. | (-∞,-2)∪(-1,0)∪(1,+∞) | C. | (-∞,0)∪(1,+∞) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com