Question

【题目】设直线l1 ， l2分别是函数f（x）= 图象上点P1 ， P2处的切线，l1与l2垂直相交于点P，且l1 ， l2分别与y轴相交于点A，B，则△PAB的面积的取值范围是（　　）
A.（0，1）
B.（0，2）
C.（0，+∞）
D.（1，+∞）

Answer 1

【答案】A
【解析】解：设P1（x1 ， y1），P2（x2 ， y2）（0＜x1＜1＜x2），当0＜x＜1时，f′（x）= ，当x＞1时，f′（x）= ，∴l1的斜率 ，l2的斜率 ，
∵l1与l2垂直，且x2＞x1＞0，
∴ ，即x1x2=1．直线l1： ，l2： ．
取x=0分别得到A（0，1﹣lnx1），B（0，﹣1+lnx2），
|AB|=|1﹣lnx1﹣（﹣1+lnx2）|=|2﹣（lnx1+lnx2）|=|2﹣lnx1x2|=2．
联立两直线方程可得交点P的横坐标为x= ，∴ |AB||xP|= = 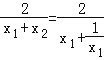．∵函数y=x+ 在（0，1）上为减函数，且0＜x1＜1，∴ ，则 ，∴ ．
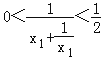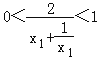∴△PAB的面积的取值范围是（0，1）．
故选：A．