
| A. | [-$\frac{\sqrt{3}}{2}$,0] | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{\sqrt{3}}{4}$,0] | D. | [-3,0] |
分析 由题意画出图形,然后建系,求出M的坐标,数形结合可得$\overrightarrow{AM}$•$\overrightarrow{BP}$的最大值为0,且可知当P在线段AC上时,$\overrightarrow{AM}$•$\overrightarrow{BP}$有最小值,设P(0,y)(0$≤y≤\sqrt{3}$),写出数量积的坐标表示,由y的范围求得最小值.
解答 解:如图,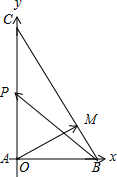
由AB=1,BC=2,可得AC=$\sqrt{3}$,
以AB所在直线为x轴,以AC所在直线为y轴,建立平面直角坐标系,
则B(1,0),C(0,$\sqrt{3}$),直线BC方程为$x+\frac{y}{\sqrt{3}}=1$,
则直线AM方程为$y=\frac{\sqrt{3}}{3}x$.
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{x+\frac{y}{\sqrt{3}}=1}\end{array}\right.$,解得:M($\frac{3}{4},\frac{\sqrt{3}}{4}$),
由图可知,当P在线段BC上时,$\overrightarrow{AM}$•$\overrightarrow{BP}$有最大值为0,
当P在线段AC上时,$\overrightarrow{AM}$•$\overrightarrow{BP}$有最小值,设P(0,y)(0$≤y≤\sqrt{3}$),
∴$\overrightarrow{AM}$•$\overrightarrow{BP}$=($\frac{3}{4},\frac{\sqrt{3}}{4}$)(-1,y)=$-\frac{3}{4}+\frac{\sqrt{3}}{4}y$$≥-\frac{3}{4}$.
∴$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是[$-\frac{3}{4},0$].
故选:B.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标运算,考查了数形结合的解题思想方法,想到建系是解答该题的关键,是中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
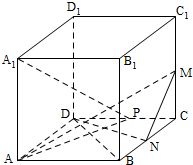
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
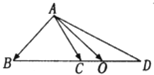 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )| A. | (-1,0) | B. | (0,$\frac{1}{3}$) | C. | (0,1) | D. | (-$\frac{1}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{17}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
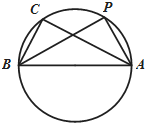 在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$.
在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
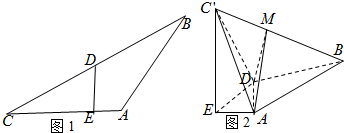
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com