练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    容积为 L(1)的容器盛满酒精后倒出1 L，然后加满水，混合溶液后再倒出1 L，又用水加满，如此继续下去，问第次操作后溶液的浓度是多少？若＝2，至少应倒出几次后才可以使酒精浓度低于10%？

    解：开始的浓度为1，操作一次后溶液的浓度是＝1－.

    设操作次后溶液的浓度是，则操作次后溶液的浓度是＝．

    所以数列是以＝1－为首项，＝1－为公比的等比数列．

    所以 ，即第次操作后溶液的浓度是.

    当＝2时，由＝，得≥4.

    因此，至少应倒4次后才可以使酒精浓度低于10%.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，斜率为1的直线过抛物线y2=2px（p＞0）的焦点，与抛物线交于两点A、B，将直线AB按向量
    a
    =(-p，0)    平移得到直线l，N为l上的动点，M为抛物线弧AB上的动点．
    （Ⅰ） 若|AB|=8，求抛物线方程．
    （Ⅱ）求S△ABM的最大值．
    （Ⅲ）求
    NA
    •
    NB
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    本题共有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则以所做的前2题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （1）选修4-2：矩阵与变换
    变换T1是逆时针旋转90°的旋转变换，对应的变换矩阵为M1，变换T2对应的变换矩阵是M2=
    11
    01
    ；
    （I）求点P（2，1）在T1作用下的点Q的坐标；
    （II）求函数y=x2的图象依次在T1，T2变换的作用下所得的曲线方程．
    （2）选修4-4：极坐标系与参数方程
    从极点O作一直线与直线l：ρcosθ=4相交于M，在OM上取一点P，使得OM•OP=12．
    （Ⅰ）求动点P的极坐标方程；
    （Ⅱ）设R为l上的任意一点，试求RP的最小值．
    （3）选修4-5：不等式选讲
    已知f（x）=|6x+a|．
    （Ⅰ）若不等式f（x）≥4的解集为{x|x≥
    1
    2
    或x≤-
    5
    6
    }    ，求实数a的值；
    （Ⅱ）在（Ⅰ）的条件下，若f（x）+f（x-1）＞b对一切实数x恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

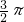    某工厂生产容积为数学公式米3的无盖圆锥形容器，容器的底面半径为r（米），而制造底面的材料每平方米30元，制造容器壁的材料每平方米20元，设计时材料厚度忽略不计．
    （1）把容器的成本y（元）表示为r的函数；
    （2）如何设计容器的尺寸，可使成本最低，最低成本是多少？（结果精确到1元）

    查看答案和解析>>

    科目：高中数学 来源：2010年安徽省高考数学最后冲刺试卷（六）（解析版） 题型：解答题

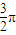    某工厂生产容积为米3的无盖圆锥形容器，容器的底面半径为r（米），而制造底面的材料每平方米30元，制造容器壁的材料每平方米20元，设计时材料厚度忽略不计．
    （1）把容器的成本y（元）表示为r的函数；
    （2）如何设计容器的尺寸，可使成本最低，最低成本是多少？（结果精确到1元）

    查看答案和解析>>

    同步练习册答案