
在△ABC中,a,b,c分别为内角A,B,C的对边,
且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
(1)A=120°;(2)当B=30°时,sinB+sinC取得最大值1.
解析试题分析:(1)根据正弦定理,设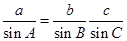 =2R,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc再与余弦定理联立方程,可求出cosA的值,进而求出A的值.
=2R,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc再与余弦定理联立方程,可求出cosA的值,进而求出A的值.
(2)根据(1)中A的值,可知c=60°-B,化简得sin(60°+B)根据三角函数的性质,得出最大值.
试题解析:(1)设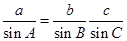 =2R
=2R
则a=2RsinA,b=2RsinB,c=2RsinC .2分
∵2asinA=(2b+c)sinB+(2c+b)sinC
方程两边同乘以2R
∴2a2=(2b+c)b+(2c+b)c 2分
整理得a2=b2+c2+bc .1分
∵由余弦定理得a2=b2+c2-2bccosA 1分
故cosA=-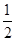 ,A=120° 2分
,A=120° 2分
(2)由(1)得:sinB+sinC=sinB+sin(60°-B) 1分
= 2分
2分
故当B=30°时,sinB+sinC取得最大值1 .1分
考点:余弦函数的应用.


科目:高中数学 来源: 题型:解答题
已知函数f(x)=msinx+ cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2.
(1)求函数f(x)在[0,π]上的单调递减区间;(2)△ABC中, 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为绘制海底地貌图,测量海底两点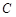 ,
, 间的距离,海底探测仪沿水平方向在
间的距离,海底探测仪沿水平方向在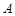 ,
,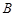 两点进行测量,
两点进行测量,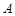 ,
,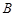 ,
,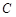 ,
, 在同一个铅垂平面内. 海底探测仪测得
在同一个铅垂平面内. 海底探测仪测得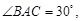

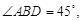
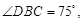
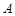 ,
,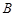 两点的距离为
两点的距离为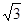 海里.
海里.
(1)求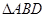 的面积;
的面积;
(2)求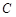 ,
, 之间的距离.
之间的距离.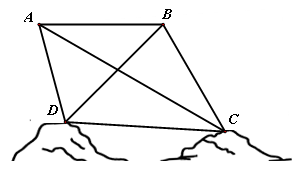
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.
(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com