
【题目】已知曲线![]() .直线
.直线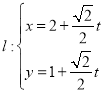 (
(![]() 为参数),点
为参数),点![]() 的坐标为
的坐标为![]() .
.
(1)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() (
(![]() 为参数);
为参数);![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆的参数方程的求法及椭圆的方程可得![]() 的参数方程,消去参数
的参数方程,消去参数![]() 即可得直线
即可得直线![]() 的普通方程;
的普通方程;
(2)法一:将直线![]() 的参数方程代入椭圆的普通方程可得关于
的参数方程代入椭圆的普通方程可得关于![]() 的一元二次方程,利用韦达定理求出
的一元二次方程,利用韦达定理求出![]() 和
和![]() ,由
,由![]() 可得
可得![]() ,
,![]() 的符合相同,进而得出
的符合相同,进而得出![]() ,即可求出
,即可求出![]() 结果;
结果;
法二:将直线![]() 的普通方程与椭圆的普通方程联立求出交点的坐标,进而利用两点间的距离公式求出
的普通方程与椭圆的普通方程联立求出交点的坐标,进而利用两点间的距离公式求出![]() 和
和![]() ,进而求得
,进而求得![]() 的值.
的值.
解:(1)曲线![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).
为参数).
直线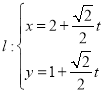 (
(![]() 为参数),消去参数
为参数),消去参数![]() 得:
得:![]() ,
,
故直线![]() 的普通方程为:
的普通方程为:![]() .
.
(2)法一:将直线![]() 的标准的参数方程代入椭圆中,
的标准的参数方程代入椭圆中,
得:![]() ,
,
整理得:![]() ,
,
![]() ,
,![]() ,可得
,可得![]() ,
,![]() 同号,
同号,
所以![]() .
.
法二:联立直线![]() 与椭圆的方程:
与椭圆的方程: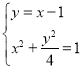 ,
,
整理得![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() ,
,
代入直线![]() 的方程可得
的方程可得![]() ,
,![]() ,
,
∴不妨设![]() ,
,![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉某商场为促进市民消费,准备每周随机的从十个热门品牌中抽取一个品牌送消费券,并且某个品牌被抽中后不再参与后面的抽奖,没有抽中的品牌则继续参加下周抽奖,假设每次抽取时各品牌被抽到的可能性相同,每次抽取也相互独立.
(1)求某品牌到第三次才被抽到的概率;
(2)为了使更多品牌参加活动,商场做出调整,从第一周抽取后开始每周会有一个新的品牌补充进抽取队伍,品牌A从第一周就开始参加抽奖,商场准备开展半年(按26周计算)的抽奖活动,记品牌A参与抽奖的次数为X,试求X的数学期望(精确到0.01).
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
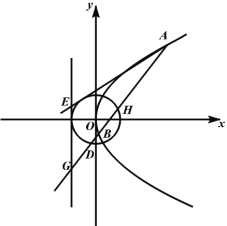
【题目】如图,在平面直角系![]() 中,点A为曲线C:
中,点A为曲线C:![]() 在第一象限的图象上的动点,点E,G在曲线C的准线
在第一象限的图象上的动点,点E,G在曲线C的准线![]() 上,且点G在x轴的下方,圆O与准线相切,直线
上,且点G在x轴的下方,圆O与准线相切,直线![]() 交曲线C于点B,交圆O于点D,H.
交曲线C于点B,交圆O于点D,H.
(1)当点H为曲线C的焦点,![]() 时,求
时,求![]() ;
;
(2)当点O为![]() 的内心时,若
的内心时,若![]() ,求点A的坐标.
,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的两切线,切点为
的两切线,切点为![]() .
.
(1)求两切点![]() 所在的直线方程;
所在的直线方程;
(2)椭圆![]() ,离心率为
,离心率为![]() ,(1)中直线AB与椭圆交于点P,Q,直线
,(1)中直线AB与椭圆交于点P,Q,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
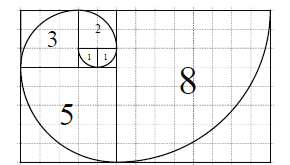
【题目】斐波那契数列![]() 满足:
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com