
分析 (1)利用导数的正负,求f (x)的单调区间;
(2)设x=$\frac{1}{n}∈(0,1]$,由(1)知:f (x)=ln(1+x)-$\frac{x}{x+1}$,f (0)=0,当x∈(0,1)时,f (x)单调递增,可得$\frac{x}{x+1}<ln(x+1)$,再来证明:当x∈(0,1)时ln(1+x)<x.构造函数m(x)=ln(x+1)-x x∈(0,1),即可证明结论;
(3)利用作差法证明an>an+1,再用放缩法证明an>0.
解答 (1)解:$f'(x)=\frac{1}{1+x}-\frac{1}{{{{(1+x)}^2}}}=\frac{x}{{{{(1+x)}^2}}}$.
令f'(x)>0,又x>-1,则x>0,
令f'(x)<0,又x>-1,则-1<x<0
故f(x)的递减区间是(-1,0),递增区间是(0,+∞)…(4分)
(2)证明:设x=$\frac{1}{n}∈(0,1]$,则$\frac{1}{n+1}<ln(\frac{1}{n}+1)<\frac{1}{n}?\frac{x}{x+1}<ln(x+1)<x$,
由(1)知:f (x)=ln(1+x)-$\frac{x}{x+1}$,f (0)=0,
当x∈(0,1)时,f (x)单调递增,∴f (x)>0,即$\frac{x}{x+1}<ln(x+1)$.
再来证明:当x∈(0,1)时ln(1+x)<x.
构造函数m(x)=ln(x+1)-x x∈(0,1),则$m'(x)=\frac{1}{x+1}-1=\frac{-x}{x+1}<0$,
故m(x)在(0,1)上递减,
∴当x∈(0,1)时,m(x)<m(0)=0,即ln(1+x)<x,
综上可知:?n∈N*有$\frac{1}{n+1}<ln(\frac{1}{n}+1)<\frac{1}{n}$.…(8分)
(3)证明:由(2)的结论知,?n∈N*有$\frac{1}{n+1}<ln(\frac{1}{n}+1)<\frac{1}{n}$
∴${a_{n+1}}-{a_n}=\frac{1}{n+1}-ln(n+1)+lnn=\frac{1}{n+1}-ln(1+\frac{1}{n})<0$
∴an>an+1
又${a_n}=1+\frac{1}{2}+…+\frac{1}{n}-lnn>ln(1+1)+ln(1+\frac{1}{2})+…+ln(1+\frac{1}{n})-lnn$
=ln2+ln$\frac{3}{2}+…+ln\frac{n+1}{n}-lnn$=ln2+(ln3-ln2)+…+[ln(n+1)-lnn]-lnn=ln(n+1)-lnn>0
综上,?n∈N*有an>an+1>0…(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
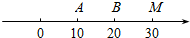 如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {2,5} | C. | {2,3,5} | D. | {2,3,5,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com