
 如图,从2009年参加奥运知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为________.
如图,从2009年参加奥运知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为________.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 +cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.
+cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.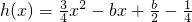 ,解不等式f'(x)+h(x)<0;
,解不等式f'(x)+h(x)<0;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
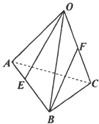 如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE=
如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE= AB,F为中点,若AB=3,BC=1,BO=2,且∠ABC=90°,∠OBA=∠OBC=60°,求异面直线OE与BF所成角的余弦值.
AB,F为中点,若AB=3,BC=1,BO=2,且∠ABC=90°,∠OBA=∠OBC=60°,求异面直线OE与BF所成角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
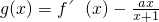 的单调区间.
的单调区间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com