
如图,在三棱锥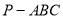 中,直线
中,直线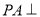 平面
平面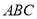 ,且
,且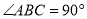 ,又点
,又点 ,
,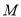 ,
,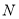 分别是线段
分别是线段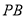 ,
,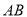 ,
, 的中点,且点
的中点,且点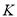 是线段
是线段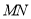 上的动点.
上的动点.
(1)证明:直线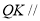 平面
平面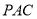 ;
;
(2)若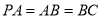 ,求二面角
,求二面角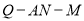 的平面角的余弦值.
的平面角的余弦值.

(1)见解析;(2)3.(3)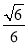
【解析】
试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明线面平行,需证线线平行,只需要证明直线的方向向量平行;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:
(1)连结QM 因为点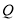 ,
,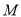 ,
,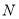 分别是线段
分别是线段 ,
,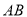 ,
,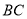 的中点
的中点
所以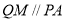 ,
,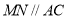
所以 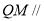 平面
平面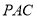 ,
, 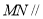 平面
平面
因为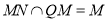 ,所以平面
,所以平面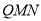 ∥平面
∥平面 ,
,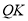
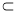 平面
平面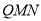
所以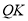 ∥平面
∥平面
(2)方法1:过M作MH⊥AN于H,连QH,则∠QHM即为
二面角 的平面角, 令
的平面角, 令
即QM=AM=1所以
此时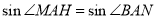
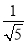 ,MH=
,MH=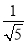 ,记二面角
,记二面角 的平面角为
的平面角为
则tan =
=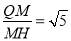 ,所以COS
,所以COS =
=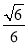 即为所求.
即为所求.
方法2:以B为原点,以BC、BA所在直线为x轴y轴建空间直角坐标系,设
则A(0,2,0),M(0,1,0),N(1,0,0),p(0,2,2),Q(0,1,1),
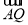 =(0,-1,1),
=(0,-1,1), 
记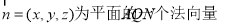 ,则
,则
取
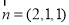
又平面ANM的一个法向量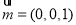 ,所以cos
,所以cos =
=
即为所求.
考点:空间几何体的线面平行以及二面角.


科目:高中数学 来源:2015届浙江省等四校高三上学期期中联考文科数学试卷(解析版) 题型:选择题
设 是实数,则“
是实数,则“ ”是“
”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届浙江省富阳市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数 的定义域为
的定义域为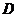 ,若存在闭区间
,若存在闭区间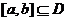 ,使得函数
,使得函数 满足:①
满足:① 在
在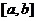 内是单调函数;②
内是单调函数;② 在
在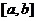 上的值域为
上的值域为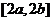 ,则称区间
,则称区间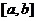 为
为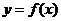 的“倍值区间”.下列函数中存在“倍值区间”的有( )
的“倍值区间”.下列函数中存在“倍值区间”的有( )
① ;
;
② ;
;
③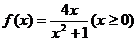 ;
;
④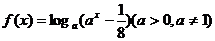
A.①②③④ B.①②④ C.①③④ D.①③
查看答案和解析>>
科目:高中数学 来源:2015届浙江省富阳市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数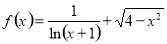 的定义域为( ).
的定义域为( ).
A.[-2,0)∪(0,2] B.(-1,0)∪(0,2] C.[-2,2] D.(-1,2]
查看答案和解析>>
科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测理科数学试卷(解析版) 题型:填空题
已知△ 中,
中, ,它所在平面外一点
,它所在平面外一点 到△
到△ 三个顶
三个顶
点的距离都是14,那么点P到平面ABC的距离为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com