
函数 的定义域为
的定义域为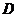 ,若存在闭区间
,若存在闭区间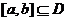 ,使得函数
,使得函数 满足:①
满足:① 在
在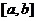 内是单调函数;②
内是单调函数;② 在
在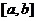 上的值域为
上的值域为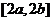 ,则称区间
,则称区间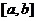 为
为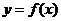 的“倍值区间”.下列函数中存在“倍值区间”的有( )
的“倍值区间”.下列函数中存在“倍值区间”的有( )
① ;
;
② ;
;
③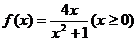 ;
;
④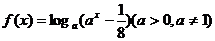
A.①②③④ B.①②④ C.①③④ D.①③
C
【解析】
试题分析:函数中存在“倍值区间”,则:① 在
在 内是单调函数;②
内是单调函数;②
① ,若存在“倍值区间”
,若存在“倍值区间” ,则
,则
∴ ,若存在“倍值区间”[0,2];
,若存在“倍值区间”[0,2];
② ,若存在“倍值区间”
,若存在“倍值区间” ,则
,则
构建函数 ,∴
,∴ ,
,
∴函数在 上单调减,在
上单调减,在 上单调增,∴函数在
上单调增,∴函数在 处取得极小值,且为最小值.
处取得极小值,且为最小值.
∵ ,∴
,∴ 恒成立,∴
恒成立,∴ 无解,故函数不存在“倍值区间”;
无解,故函数不存在“倍值区间”;
③因为 ,所以
,所以
若存在“倍值区间”
 ,则
,则 ,若存在“倍值区间”
,若存在“倍值区间” ;
;
④ )(a>0,a≠1).不妨设
)(a>0,a≠1).不妨设 ,则函数在定义域内为单调增函数
,则函数在定义域内为单调增函数
若存在“倍值区间” ,则
,则 必有m,n是方程
必有m,n是方程 的两个根,必有m,n是方程
的两个根,必有m,n是方程 的两个根,由于
的两个根,由于 存在两个不等式的根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④
存在两个不等式的根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④
考点:函数单调性、函数的定义域、函数的值域 .


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届浙江省新高考单科综合调研卷文科数学试卷一(解析版) 题型:填空题
已知抛物线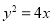 的准线与双曲线
的准线与双曲线 交于
交于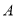 、
、 两点,点
两点,点 为抛物线的焦点,若
为抛物线的焦点,若 为直角三角形,则双曲线离心率的取值范围是 .
为直角三角形,则双曲线离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省富阳市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(12分)已知函数 (
( 是不为零的实数,
是不为零的实数, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 与
与 有公共点,且在它们的某一公共点处有共同的切线,求
有公共点,且在它们的某一公共点处有共同的切线,求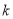 的值;
的值;
(2)若函数 在区间
在区间 内单调递减,求此时
内单调递减,求此时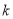 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省富阳市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
如图,在三棱锥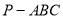 中,直线
中,直线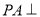 平面
平面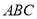 ,且
,且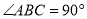 ,又点
,又点 ,
,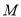 ,
,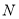 分别是线段
分别是线段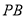 ,
,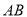 ,
, 的中点,且点
的中点,且点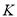 是线段
是线段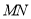 上的动点.
上的动点.
(1)证明:直线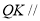 平面
平面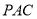 ;
;
(2)若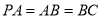 ,求二面角
,求二面角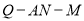 的平面角的余弦值.
的平面角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com