Question

8．已知a∈R，函数f（x）=x|x-a|，
（Ⅰ）当a=2时，作出图形并写出函数y=f（x）的单调递增区间；
（Ⅱ）当a=-2时，求函数y=f（x）在区间$（-\sqrt{2}-1，2]$的值域；
（Ⅲ）设a＞0，函数f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围（用a表示）．

Answer 1

分析 （Ⅰ）当a=2时，化简函数解析式，作出图形并写出函数y=f（x）的单调递增区间．
（Ⅱ）利用函数的图象判断函数在（-2，-1）是减函数，在（-1，2）是减函数，求出函数的最值．
（Ⅲ）化简函数$f（x）=\left\{\begin{array}{l}x（x-a），x≥a\\ x（a-x），x＜a\end{array}\right.$，画出图象，利用最值，求解范围即可．

解答 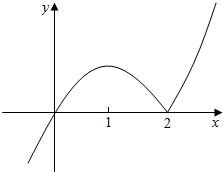（Ⅰ）解：当a=2时，f（x）=x|x-2|=$\left\{\begin{array}{l}x（x-2），x≥2\\ x（2-x），x＜2\end{array}\right.$，作出图象  …（2分）
由图象可知，
单调递增区间为（-∞，1]，[2，+∞）…（4分）
（Ⅱ）∵$f（x）在（-\sqrt{2}-1，-2）$是增函数，在（-2，-1）是减函数，在（-1，2）是减函数，…（6分）
∴f（x）_min=f（-1）=-1∴f（x）_max=8…（8分）
∴f（x）的值域为[-1，8]…（10分）
（Ⅲ）$f（x）=\left\{\begin{array}{l}x（x-a），x≥a\\ x（a-x），x＜a\end{array}\right.$
当a＞0时，图象如图所示
由$\left\{\begin{array}{l}y=\frac{a^2}{4}\\ y=x（x-a）\end{array}\right.$得$x=\frac{{（\sqrt{2}+1）a}}{2}$…（12分）
∴$0≤m＜\frac{a}{2}$，$a＜n≤\frac{{\sqrt{2}+1}}{2}a$…（16分）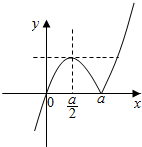

点评 本题考查函数的解析式的化简，图象的作法，函数的最值的解法，考查转化思想以及计算能力．