
| A. | $\frac{10}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
分析 通过等差数列的性质可得S3、S6-S3、S9-S6、S12-S9成等差数列,利用$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$计算即得结论.
解答 解:∵等差数列{an}的前n项和为Sn,
∴S3、S6-S3、S9-S6、S12-S9成等差数列,
又∵$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$,
∴S6=3S3,
∴(S6-S3)-S3=S3,
S9-S6=(S6-S3)+S3=S6=3S3,
S12-S9=(S9-S6)+S3=4S3,
∴(S12-S9)+(S9-S6)=S12-S6=7S3,
∴S12=S6+7S3=3S3+7S3=10S3,
∴$\frac{S_6}{{{S_{12}}}}$=$\frac{3{S}_{3}}{10{S}_{3}}$=$\frac{3}{10}$,
故选:B.
点评 本题考查等差数列的性质,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
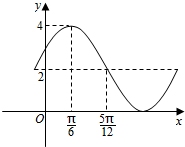 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 | B. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | ||
| C. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≤2 | D. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com