
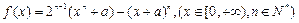 求函数
求函数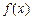 的最小值;
的最小值;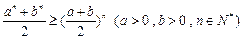 ;
;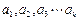 均为正数,则有
均为正数,则有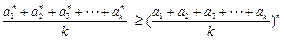 成立(其中
成立(其中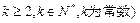 .请你构造一个函数
.请你构造一个函数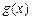 ,证明:
,证明: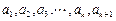 均为正数时,
均为正数时,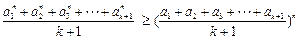 .
.科目:高中数学 来源:不详 题型:解答题
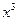 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数. ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f( ))=
))= ,求证:f(
,求证:f( )=
)= .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
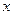 与人均消费
与人均消费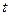 (元)的关系如下:
(元)的关系如下: 
 万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?
万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
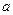
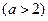 ,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。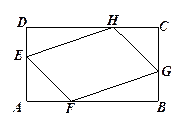
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
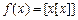 ,其中
,其中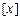 表示不超过x的最大整数,如:
表示不超过x的最大整数,如: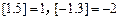 ,当
,当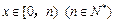 时,设函数
时,设函数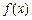 的值域为A,记集合A中的元素个数为an,则式子
的值域为A,记集合A中的元素个数为an,则式子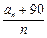 的最小值为( )
的最小值为( )| A.10 | B.13 | C.14 | D.16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com