
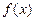 是定义在
是定义在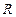 上的偶函数,当
上的偶函数,当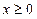 时,
时,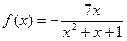 .
.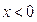 时
时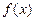 的解析式;
的解析式;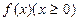 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;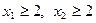 且
且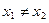 ,证明:
,证明: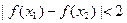 .
.科目:高中数学 来源:不详 题型:解答题
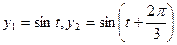 和
和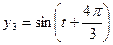 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
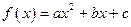 .
.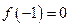 ,试判断函数
,试判断函数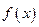 零点个数;
零点个数;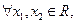 且
且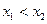 ,
,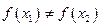 ,试证明
,试证明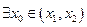 ,使
,使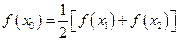 成立。
成立。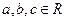 ,使
,使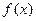 同时满足以下条件①对
同时满足以下条件①对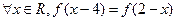 ,且
,且 ;②对
;②对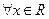 ,都有
,都有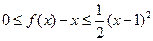 。若存在,求出
。若存在,求出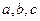 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
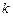 和
和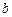 ,使得函数
,使得函数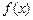 和
和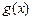 对其定义域上的任意实数
对其定义域上的任意实数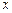 分别满足:
分别满足: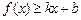 和
和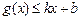 ,则称直线
,则称直线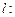
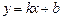 为
为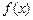 和
和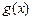 的“隔离直线”.已知
的“隔离直线”.已知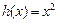 ,
,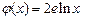 (其中
(其中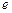 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断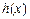 与
与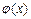 间的隔离直线方程为 .
间的隔离直线方程为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com