
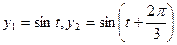 和
和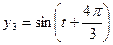 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由科目:高中数学 来源:不详 题型:解答题
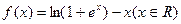 有下列性质:“若
有下列性质:“若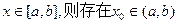 ,使得
,使得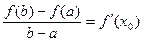 ”成立。
”成立。 唯一;
唯一; 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
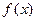 与产量
与产量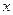 之间的关系式为
之间的关系式为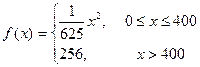 ,每件产品的售价
,每件产品的售价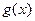 与产量
与产量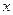 之间的关系式为
之间的关系式为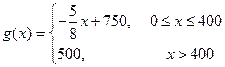 .
. 与产量
与产量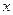 之间的关系式;
之间的关系式;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com