
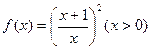 .
.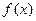 的反函数
的反函数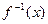 ;
;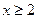 时,不等式
时,不等式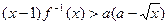 恒成立,试求实数
恒成立,试求实数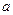 的范围.
的范围.科目:高中数学 来源:不详 题型:解答题
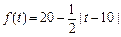 (元).
(元).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是函数
是函数 的一个极值,称点
的一个极值,称点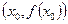 是函数
是函数 的一个极值点.已知函数
的一个极值点.已知函数
 总存在有两个极值点
总存在有两个极值点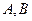 ,求
,求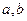 所满足的关系;
所满足的关系; 有两个极值点
有两个极值点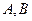 ,且存在
,且存在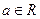 ,求
,求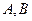 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数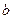 的范围.
的范围. 恰有一个极值点
恰有一个极值点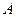 ,且存在
,且存在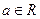 ,使
,使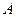 在不等式
在不等式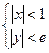 表示的区域内,证明:
表示的区域内,证明: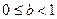 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
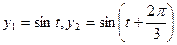 和
和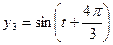 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
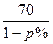 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
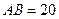 km,
km, 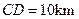 ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。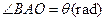 ,将
,将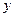 表示成
表示成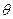 的函数关系式;
的函数关系式;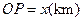 ,将
,将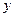 表示成
表示成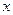 的函数关系式。
的函数关系式。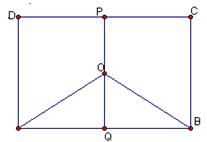
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 艘产值函数为
艘产值函数为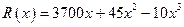 (单位:万元),成本函数
(单位:万元),成本函数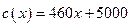 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数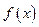 的边际函数
的边际函数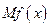 定义为
定义为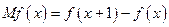
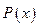 及边际利润函数
及边际利润函数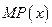 (利润=产值—成本)
(利润=产值—成本)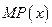
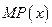 的单调递减区间
的单调递减区间查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
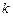 和
和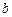 ,使得函数
,使得函数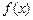 和
和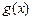 对其定义域上的任意实数
对其定义域上的任意实数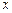 分别满足:
分别满足: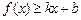 和
和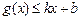 ,则称直线
,则称直线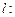
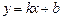 为
为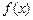 和
和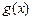 的“隔离直线”.已知
的“隔离直线”.已知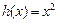 ,
,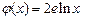 (其中
(其中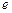 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断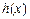 与
与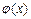 间的隔离直线方程为 .
间的隔离直线方程为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com