
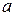 为实数,函数
为实数,函数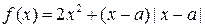 .
.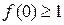 ,求
,求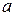 的取值范围;
的取值范围;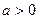 写出
写出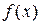 的单调递减区间;
的单调递减区间;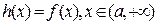
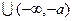 且
且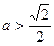 求不等式
求不等式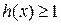 的解集.
的解集. 科目:高中数学 来源:不详 题型:解答题
 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
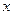 m处的大气压强是
m处的大气压强是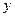 Pa,
Pa,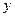 与
与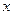 之间的函数关系式是
之间的函数关系式是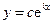 ,其中
,其中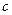 ,
,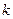 为常量.测得某地某天海平面的大气压强为
为常量.测得某地某天海平面的大气压强为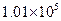 Pa,1000m高空的大气压为
Pa,1000m高空的大气压为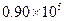 Pa,求600m高空的大气压强(保留
Pa,求600m高空的大气压强(保留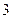 个有效数字).
个有效数字).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com